弧の長さと面積(説明ページ)
概要
半径 r、中心各 a° のおうぎ形の弧の長さと面積は以下のように表せる。
- 弧の長さ(ℓ):2πr × a360
- 面積(S):πr2 × a360
円周率(π)
小学校では円の面積は「半径×半径×円周率(3.14)」と学んできたかと思いますが、実は円周率は厳密には3.14ではありません。
円周率は3.14159265359…であり、これを小数第二位までの3.14として計算していたのです。
そこで、今後は円周率を表す文字として、ギリシャ文字のπ(パイ)を使用していきます。
つまり、半径をrとすると、円の面積は、
「半径(r)×半径(r)×円周率(π)」=πr2
と表すことが出来ます。(r2πでもいいのですが、πr2と書く慣習があります。)
同様に、円周は
「2×半径(r)×円周率(π)」=2πr
と表すことが出来ます。(2rπでもいいのですが、2πrと書く慣習があります。)
とりあえずこれだけ覚えて!
- 円周率はπという文字で表す(π=3.14159265359…)
- 半径 r の円の周の長さ(ℓ)と面積(S)は
- 円周(ℓ):2πr
- 面積(S):πr2
練習問題1
半径5の円の周の長さと面積を求めなさい。
円周:××=
面積:××=
おうぎ形の面積と弧の長さ
おうぎ形の面積と弧の長さは、中心角の大きさに比例するので、以下のように表せます。
とりあえずこれだけ覚えて!
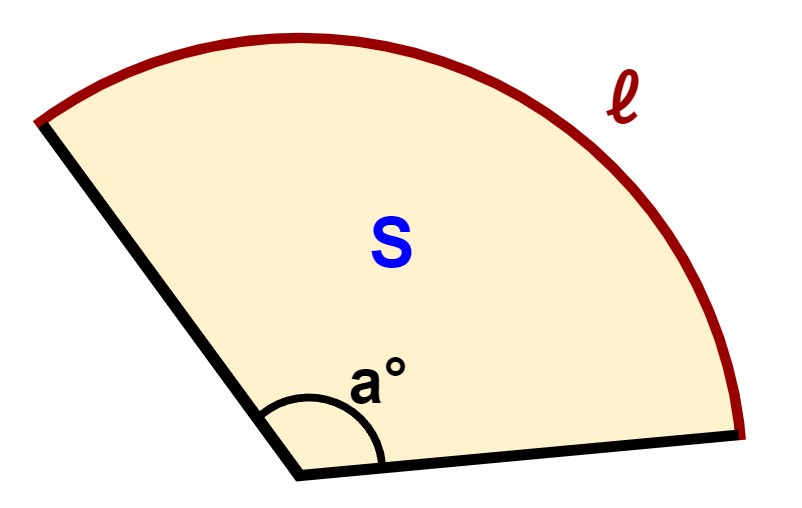
半径 r、中心各 a° のおうぎ形の弧の長さ(ℓ)と面積(S)は以下のように表せる。
- 弧の長さ(ℓ):2πr × a360
- 面積(S):πr2 × a360
(注目)a°が360°の時は円の面積と円周の公式と等しくなります。(中心角360°のおうぎ形は円と等しいため)
練習問題2
半径6、中心角120°のおうぎ形の弧の長さと面積を求めなさい。
弧の長さ
×××
=×
=
面積
×××
=×
=
また、半径 r、中心各 a° のおうぎ形の弧の長さ(ℓ)と面積(S)は以下のように表せることから、
- 弧の長さ(ℓ):2πr × a360
- 面積(S):πr2 × a360
弧の長さ(ℓ)と面積(S)には以下の関係が成り立つことも知られています。
とりあえずこれだけ覚えて!
面積(S):弧の長さ(ℓ)× r ×12
練習問題3
半径6、弧の長さが4πのおうぎ形の面積を求めなさい。
××
=