素数(説明ページ)
概要
- 1とその数自身以外に約数がない自然数を素数という。
- ただし、1は素数にふくめない。
- 自然数を素数の積で表すことを、素因数分解という。
素数
1とその数自身以外で、割ることができない数を素数と言います。
例えば、「2,3,5,7,11,13」などが素数です。
何が素数で何が素数じゃないのかは、具体例を見た方がわかりやすいと思うので、例題で解説していきます。
例題1(問題)
次の数が素数かどうかを答えなさい。
(1)6
(2)5
例題1(解説)
(1)
6が素数であるかを確認する。
- 6が6より小さい数(1以外)で割り切ることができるかを確認します。
- 6÷2=3、6÷3=2です。
- つまり、6は6より小さい数で割り切ることができます。
- このような数は素数とは言いません。
答え:素数ではない
(2)
5が素数であるかを確認する。
- 5が5より小さい数(1以外)で割り切ることができるかを確認します。
- 5÷4=1あまり1、5÷3=1あまり2、5÷2=2あまり1 です。
- つまり、5は5より小さい数で割り切ることができません。
- このような数を素数と言います。
答え:素数である
なれるために、練習問題を解いていきましょう。
練習問題1(問題)
次の数が素数かどうかを答えなさい。
(1)7
(2)4
練習問題1(解説)
(1)
7が素数であるかを確認する。
- 7が7より小さい数(1以外)で割り切ることができるかを確認します。
- 7÷6=1あまり1、7÷5=1あまり2、7÷4=1あまり3、7÷3=2あまり1、7÷2=3あまり1 です。
- つまり、7は7より小さい数で割り切ることができません。
- このような数を素数と言います。
答え:素数である
(2)
4が素数であるかを確認する。
- 4が4より小さい数(1以外)で割り切ることができるかを確認します。
- 4÷2=2 です。
- つまり、4は4より小さい数で割り切ることができます。
- このような数は素数とは言いません。
答え:素数ではない
素因数分解
自然数を素数の積で表すことを、素因数分解といいます。
例えば12を素因数分解すると、以下のようになります。
12=2×2×3=22×3(2も3も素数である)
これが、素因数分解です。
例えば、以下のようにも表現することはできますが、4は素数ではないので、これでは素因数分解ではありません。
12=4×3(4は素数ではない)
なれるまでは素因数分解をスムーズにできないかもしれませんが、練習問題でなれていってください。
練習問題2(問題)
次の数を素因数分解しなさい。
(1)30
(2)28
練習問題2(解説)
(1)
30を素因数分解する。
- 30がどのような素数で割り切ることができるかを考えます。
例えば、2で割り切れることに気づいたとします。 - 30=15 × 2 (2は素数だけど、15 は素数ではない)
- 15 がどのような素数で割り切ることができるかを考えます。
例えば、3で割り切れることに気づいたとします。 - 15=3×5(3も5も素数である)
- つまり、30=15 ×2=3×5×2である。
※ この計算を、わり算のひっ算のように計算する方法が一般的ですのです。好きな方法で計算しましょう。
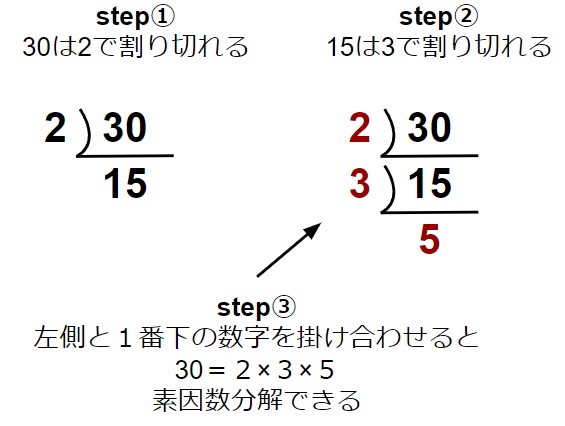
答え:30=3×5×2
(2)
28を素因数分解する。
- 28がどのような素数で割り切ることができるかを考えます。
例えば、2で割り切れることに気づいたとします。 - 28=14 × 2 (2は素数だけど、14 は素数ではない)
- 14 がどのような素数で割り切ることができるかを考えます。
例えば、また2で割り切れることに気づいたとします。 - 14=7×2(7も2も素数である)
- つまり、28=14 ×2=7×2×2=7×22である。
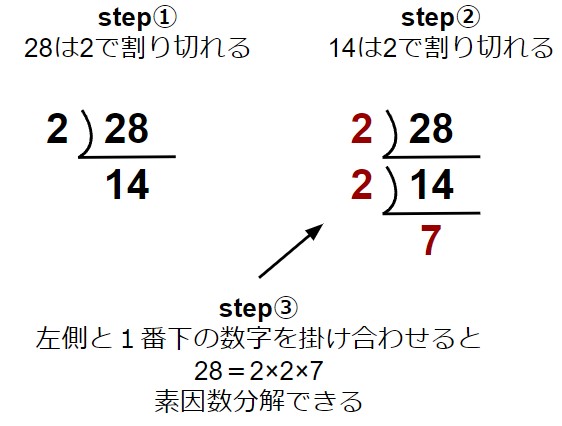
答え:28=7×22