負の数の計算(+/-)(説明ページ)
概要
負の数を使った足し算・引き算はまずは数直線を使って考えると理解しやすい。
慣れてきたら数直線を書かずに解けるようになるとよい。
目次
負の数の考え方
いきなりですが、負の数(-)を計算するときは「逆」になる。という呪文をまずは覚えてください。
「逆」になるとは、どういうことかは後で説明しますが、まずは「逆」になるんだ~という程度で読み進めてください。
とりあえずこれだけ覚えて!
- 負の数(-)を計算するときは「逆」になる
※数学的な表現ではないですが、今後大事な考えになってくるので一旦は受け入れてください、、
数直線を用いた計算
数直線を使うと、負の数を使った足し算・引き算が理解しやすくなるため、まずは数直線を用いて考えてみます。
例えば、(-1) + 6 を計算してみましょう。
考え方
(-1) + 6 を計算する
- 日本語で考える。
(-1) に 6 を足している - 数直線で(-1)を作図する。
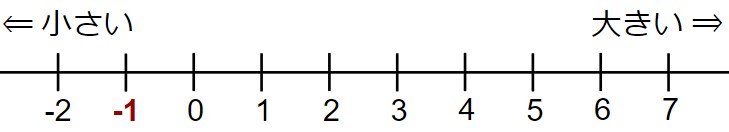
- 「6を足す」ということは、「6大きくする」ということと同じ。
- 数直線上で「6大きくする」=「6つ右に移動する」
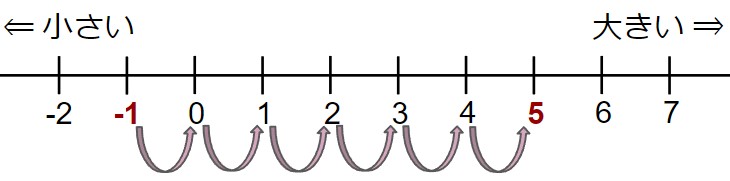
答え:5
同じように、1 + (-5) を計算してみましょう。
考え方
1 + (-5) を計算する
- 日本語で考える。
1に (-5) を足している - 数直線で1を作図する。
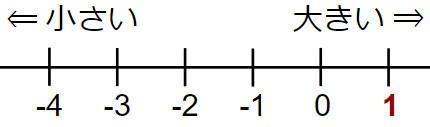
- 「(-5) を足す」ということは、どいうことだろうか?
ここで、負の数(-)を計算するときは「逆」になるという呪文が登場する。
「(-5) を足す」ということは、つまり「 5 を引く」ということになる。
※(-)の記号の影響で、「足す」が「引く」になったと考えてください。 - 「5を引く」ということは、「5小さくする」ということと同じ。
- 数直線上で「5小さくする」=「5つ左に移動する」
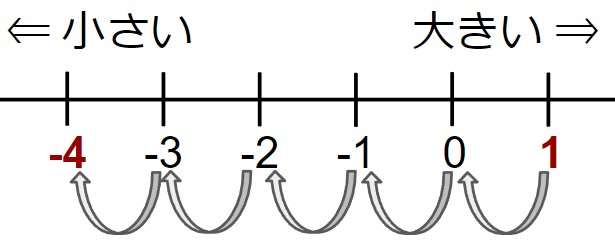
答え:-4
数学用語の暗記
これからよく登場する以下の用語を覚えてください。
とりあえずこれだけ覚えて!
- 足し算のことを、数学用語で「加法」という。
- 引き算のことを、数学用語で「減法」という。
少し難しそうな言い方をしているだけで、みなさんが知っている足し算、引き算のことです。
練習問題1(問題)
次の空欄を埋めなさい。
足し算のことを、数学用語で「」という。
引き算のことを、数学用語で「」という。
数直線を用いずに計算
実は、負の数を用いた計算(加法/減法)は、すべて数直線を用いてとくことができます。
※ 教科書には、「同じ符号同士の計算の時は符号はそのままで絶対値を足し合わせる」「違う符号での計算の時は絶対値の差を取り、符号は絶対値の大きい方を採用する」といった”ルール”が紹介されているかもしれませんが、最初は混乱してしまうと思います。このルールを覚えるだけでは意味がないので、まずは頭の中で数直線をイメージしながら暗算できるようになりましょう。
以下に練習問題を用意しましたので、負の数の加法/減法になれていってください。
練習問題2(問題)
次の計算をしなさい。
問題A:(-5) + 3=
問題B:(-1) + (-3)=
問題C:(+5) - (-3)=
練習問題2(解説)
問題A
(-5) + 3 を計算する
- 日本語で考える。
(-5) に3 を足している - 数直線で (-5) を作図する。
- 「3を足す」ということは、「3大きくする」ということと同じ。
- 数直線上で「3大きくする」=「3つ右に移動する」
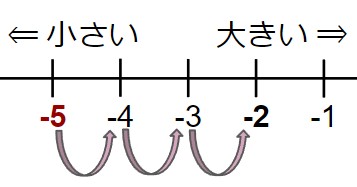
答え:-2
問題B
(-1) + (-3) を計算する
- 日本語で考える。
(-1) に (-3) を足している - 数直線で (-1) を作図する。
- 「(-3) を足す」ということは、つまり「3を引く」ということになる。
※ 負の数(-)を計算するときは「逆」になる
※(-)の記号の影響で、「足す」が「引く」になったと考えてください。 - 「3を引く」ということは、「3小さくする」ということと同じ。
- 数直線上で「3小さくする」=「3つ左に移動する」
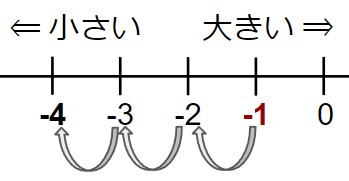
答え:-4
問題C
(+5) - (-3) を計算する
- 日本語で考える。
(+5) から (-3) を引いている - 数直線で (+5) 、つまり5を作図する。
- 「(-3) を引く」ということは、つまり「3を足す」ということになる。
※ 負の数(-)を計算するときは「逆」になる
※(-)の記号の影響で、「引く」が「足す」になったと考えてください。 - 「3を足す」ということは、「3大きくする」ということと同じ。
- 数直線上で「3大きくする」=「3つ右に移動する」
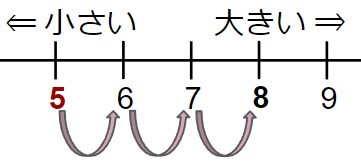
答え:8
練習問題3(問題)
問題A:(-0.2) + 0.5問題B:(-23) -(-13)
問題C:(-23) +12
練習問題3(解説)
少し応用問題ではあるが、やることは同じである。
問題A
(-0.2) + 0.5 を計算する
- 日本語で考える。
(-0.2) に0.5 を足している - 数直線で (-0.2) を作図する。
- 「0.5を足す」ということは、「0.5大きくする」ということと同じ。
- 数直線上で「0.5大きくする」=「0.5つ右に移動する」
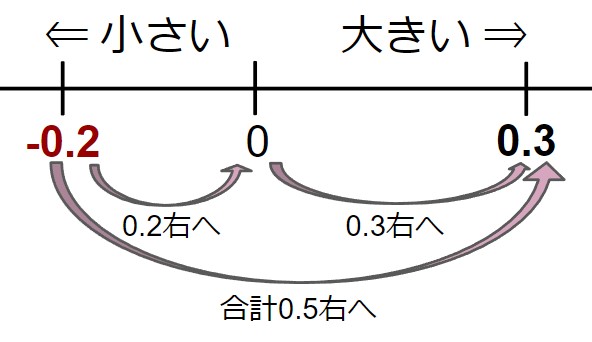
答え:0.3
問題B
-
日本語で考える。
(-23)から(-13)を引いている。 - 数直線で(-23)を作図する。
-
「(-13)を引く」ということは、つまり「13を足す」と言うことになる。
※負の数(-)を計算するときは「逆」になる
※(-)の記号の影響で、「引く」が「足す」になったと考えてください。 - 「13を足す」ということは、「13大きくする」と言うことと同じ。
- 数直線上で「13大きくする」=「13右に移動する」
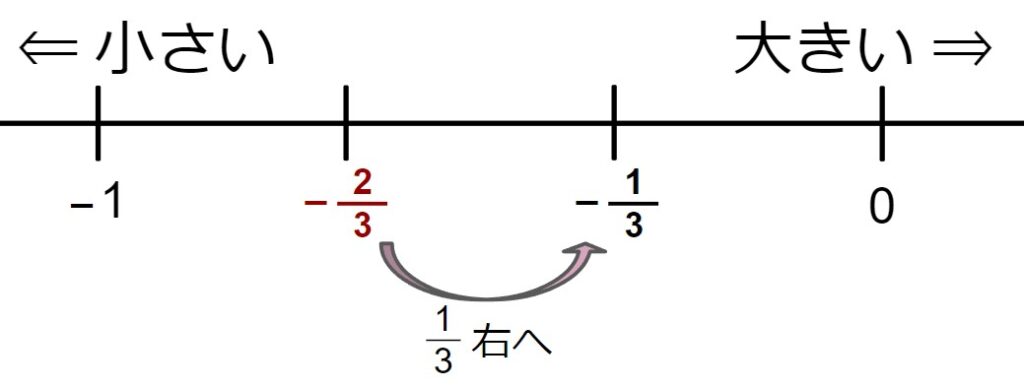
問題C
-
通分しないと分数の計算ができないので通分をする。
(-23)+12
⇒(-46)+36 -
日本語で考える。
(-46)に36を足している。 - 数直線で(-46)を作図する。
- 「36を足す」ということは、「36大きくする」と言うことと同じ。
- 数直線上で「36大きくする」=「36右に移動する」