文字式の応用（説明ページ）

文字式の利用する意味

文字式を利用する意味は、文字式の範囲ですでに勉強しています。

「物事の関係性を１つの式で表すことが出来る」

というメリットがあるため文字式を利用するのです。

ここでは、文字式の応用として、色々な事象や関係を文字式で表すことで、文字式のメリットを改めて確認していきましょう。

文字式を使わなかった場合

まずは、文字式を使わない状態で、「２つの連続する整数の和は、奇数である」が正しいかどうかを確認してみましょう。

まず、適当に連続する整数を２つ足し合わせてみましょう。

• 1＋2＝3（奇数）
• 3＋4＝7（奇数）
• 5＋6＝11（奇数）
• 11＋12＝23（奇数）

と、確かに２つの連続する整数の和が奇数であることが分かります。

しかし、この関係がすべての整数に当てはまるかどうか、を確認するためには無限に数を足し合わせ続けないといけません。

文字式を使った場合

次に、文字式を使ってみるとどうでしょうか。

まず、１つ目の整数を「ｘ」と置くと、２つ目の整数は「ｘ＋１」と置くことが出来ます。

この２つの整数を足してみると

　ｘ＋（ｘ＋１）＝２x＋１

となります。

ここで、偶数と奇数の定義を思い出してみると

• 偶数・・・２で割り切れる数
• 奇数・・・２で割り切れない数

ですので、２x＋１は２で割り切れないことから奇数であることが分かります

つまり、２つの連続する整数「x」と「x＋１」の和「2x＋1」は奇数である。

と文字式を使用することでこの関係がすべての整数に当てはまることを確認できました。

文字式の利用

「２つの奇数の和は、偶数である」という事実を文字式で確認してみましょう。

まずは、先ほども出てきましたが、

• 偶数・・・２で割り切れる数
• 奇数・・・２で割り切れない数

という関係から、２つの奇数を２m＋１、２n＋１と表します。（m、n は整数を表す文字）

次に、この２つの奇数の和を求めると

　（２m＋１）＋（２n＋１）

　＝２ｍ＋２ｎ＋２

　＝２（ｍ＋ｎ＋１）

となり、２で割り切れる式になったことから、「２つの奇数の和は、偶数である」という事実が確認できた。

まとめると、

• ２つの奇数を、２m＋１、２n＋１と表す。（m、n は整数を表す文字）
• この２つの奇数を足すと（２m＋１）＋（２n＋１）＝２（ｍ＋ｎ＋１）となる。
• m、n は整数なので、２（ｍ＋ｎ＋１）は、２×（整数）であるため、偶数を表している。
• つまり、２つの奇数の和は、偶数である

文字式の変形

文字式の利用の応用として、次は文字式の変形について説明します。

突然ですが、以下の三角形の高さを求めてみましょう。

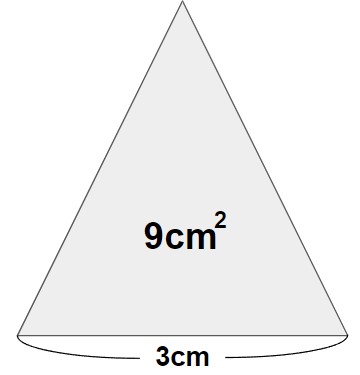
まず、三角形の面積（S）と底辺（a）と高さ（h）の関係は、

  S＝12ah・・・①

ですので、いきなり S=9、a=3を代入してもいいですが、実は最初に以下のように式を変形しておくと便利です。

式①の両辺を2a倍し、
  S×2a＝h
つまり、
  h＝2Sa

この式に、S=9、a=3を代入すると、

  h＝293＝6

つまり、高さは６であることが求まりました。

このように、はじめの式①を「ｈ＝」の形に変形することを、「式①をｈについて解く」と言います。

練習問題１

次の式を a について解きなさい。

（１）h＝a＋b
両辺からbを引いて
h-b＝a+b-b=a
つまり、
a＝h-b

（２）2ab＝c
両辺に12bをかけて
2ab×12b＝c2b
つまり、
a＝c2b