方程式（説明ページ）

方程式

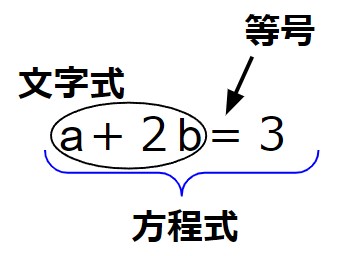
文字式を含んだ等式のことを方程式といいます。

等式を忘れてしまった人のために復習すると、
「＝」のことを等号といい、等号「＝」を使った式のことを等式といいます。

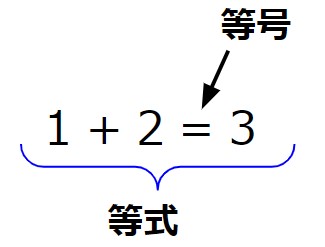
そして、文字式を含んだ等式のことを方程式といいます。

練習問題１（問題）

文字式を含んだ等式のことを方程式という。

一元一次方程式

方程式の中でも、1種類の文字しか登場せず、また、累乗（x²や a³）が登場しないもののことを一元一次方程式といいます。
※一元一次方程式の「一元」は「1種類の文字しか登場しない」ということを、「一次」は「3aやx+yなど、累乗（x²や a³）が登場しない」ということを意味します。

例えば、 ２a－４=0 は1種類の文字（a）しか登場せず、累乗も登場しないので一元一次方程式です。

一方、x+y=3 は、2種類の文字（xとy）が登場するので一元一次方程式ではありません。
また、x²＋２x＝5 は、１種類の文字（x）しか登場しませんが、累乗（x²）が登場するので、一元一次方程式ではありません。

練習問題２（問題）

方程式の中でも、1種類の文字しか登場せず、また、累乗（x²や a³）が登場しないもののことを一元一次方程式という。

方程式を解くとは

例えば、さきほども例に挙げた以下の方程式を例にとります。

この方程式に、a＝１、b＝２を代入すると
　1＋2×２ ＝１＋４＝３（※１＋４は本当は５だから間違っている）
と、式が成り立ちません。

一方、この方程式に、a＝１、b＝１を代入すると
　1＋2×1 ＝１＋２＝３
と、式が成り立ちます。

このように、方程式が成り立つように、文字に入る値を見つけることを、方程式を解くといいます。
つまり、今回の例でいうと「a=1, b=1という値を見つけること」を方程式を解くといいます。
また、a=1, b=1 のように、方程式を成り立たせる文字の値のことを、方程式の解といいます。
※a+2b=3にはa=1,b=1以外にも複数の解が存在する。

練習問題３（問題）

方程式を成り立たせる文字の値を方程式の解という。
解を見つけることを、方程式を解くという。