平面図形の用語説明(円以外)(説明ページ)
概要
平面図形の範囲では、覚えないといけない用語が多く登場します。
まずは用語を覚えるところから始めましょう。
目次
直線・半直線・線分
直線とは無限に続くまっすぐな線です。
半直線とは片方に終わりがあり(無限に続かず)、もう片方が無限に続くまっすぐな線です。
線分とは、無限に続かないまっすぐな線です。
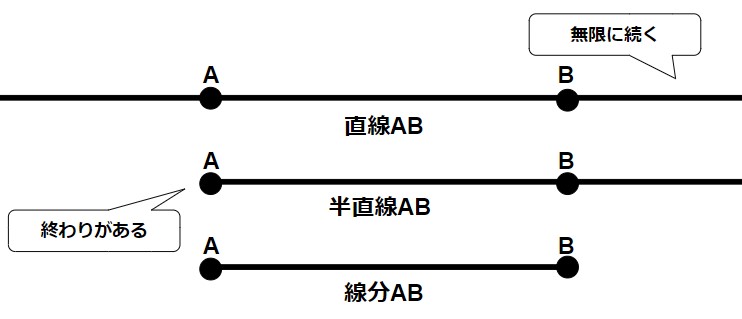
点Aと点Bを通過する直線、半直線、線分をそれぞれ直線AB、半直線AB、線分ABと呼びます。
また、これら3つとも、アルファベットだけで「AB」と表すこともあります。
角度(∠)
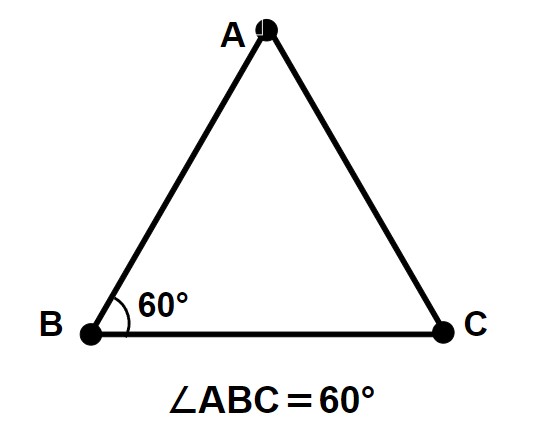
「∠」 は角度を表す記号であり、例えば下図のような三角形の頂点Bの角度は、 ∠ABCと表します。
三角形 (△)
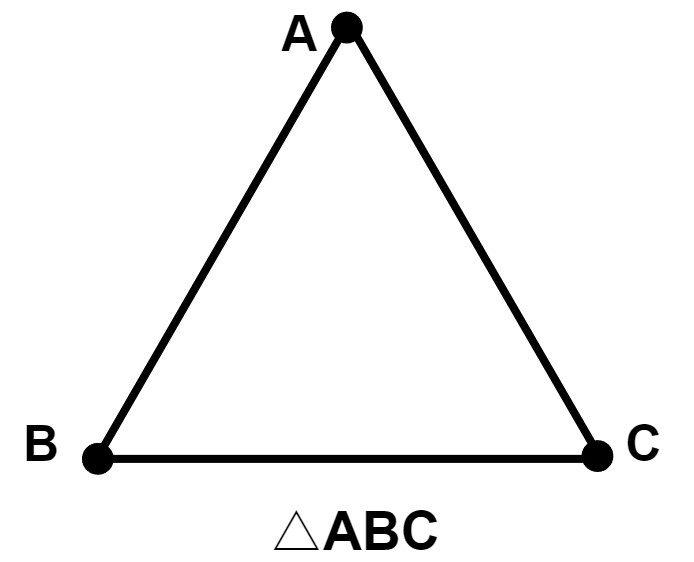
「△」 は三角形を表す記号であり、例えば下図のような三角形は△ABCと表します。
垂直(⊥)・垂線
ABとCDが90度に交わっているとき、ABとCDは垂直であるといいます。
「⊥」は2直線が垂直であることを表す記号であり、例えば以下の図の状態はAB⊥CDと表します。
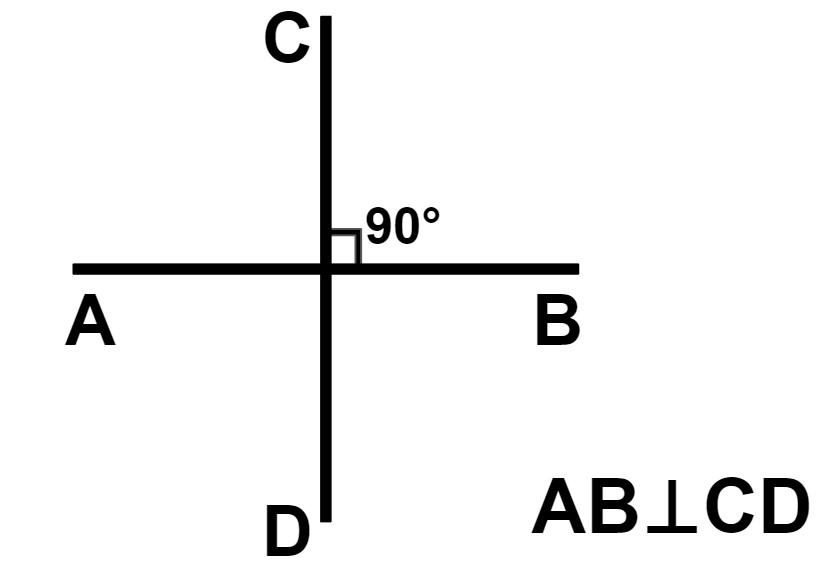
また、ある直線に垂直な線を垂線と言います。
例えば、「CDはABの垂線である(ABはCDの垂線である)」という言い方をします。
平行(//)
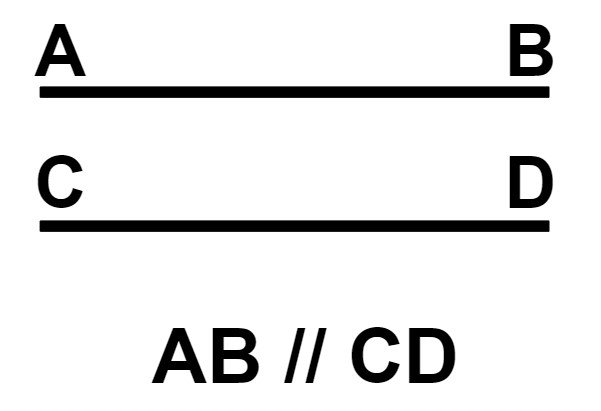
ABとCDが、どれだけ伸ばしても交わらないとき、ABとCDは平行であるといいます。
「//」は2直線が平行であることを表す記号であり、例えば以下の図の状態はAB//CDと表します。
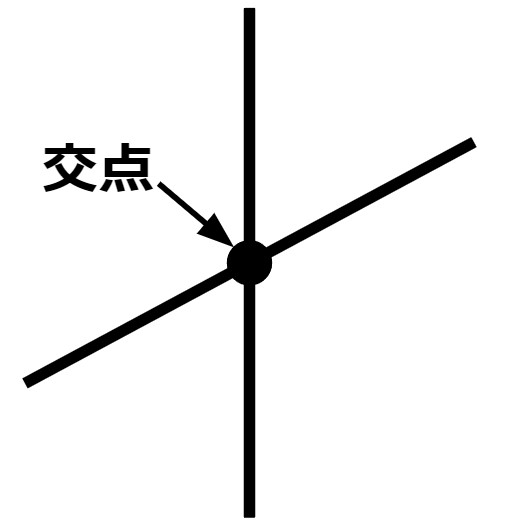
交点
線と線が交わる点を交点といいます。
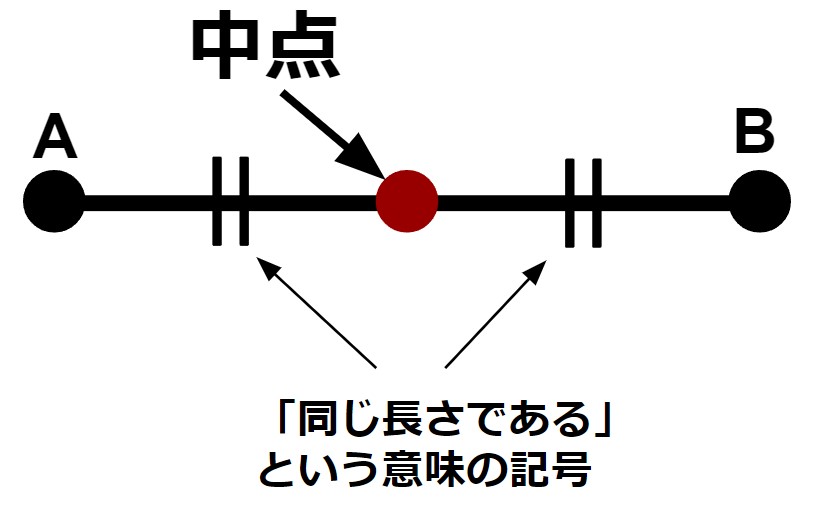
中点
線分のちょうど真ん中の点を中点といいます。
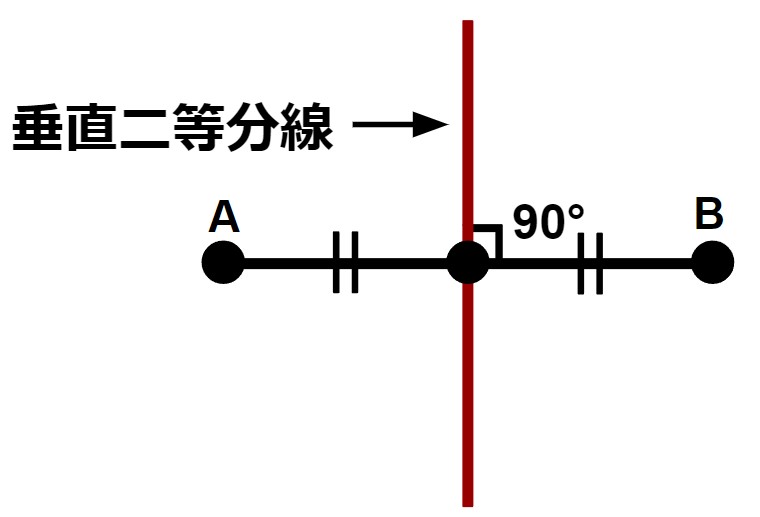
垂直二等分線
中点を通る垂線のことを垂直二等分線といいます。
角の二等分線
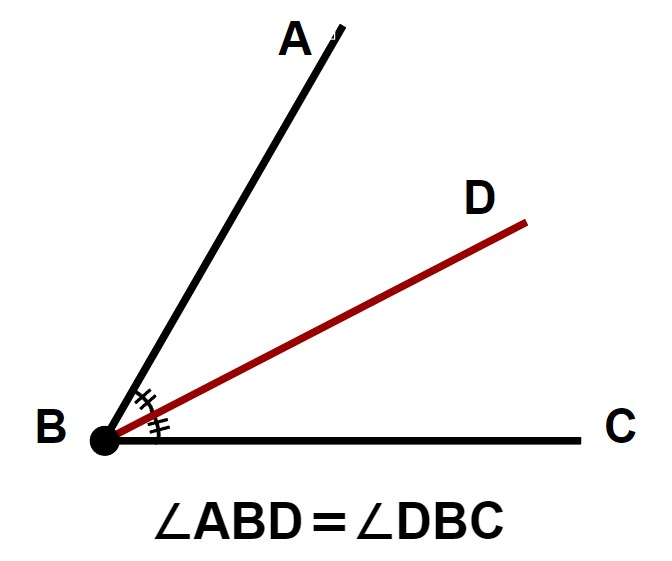
角度をちょうど半分にする(2等分する)半直線を角の二等分線といいます。
距離
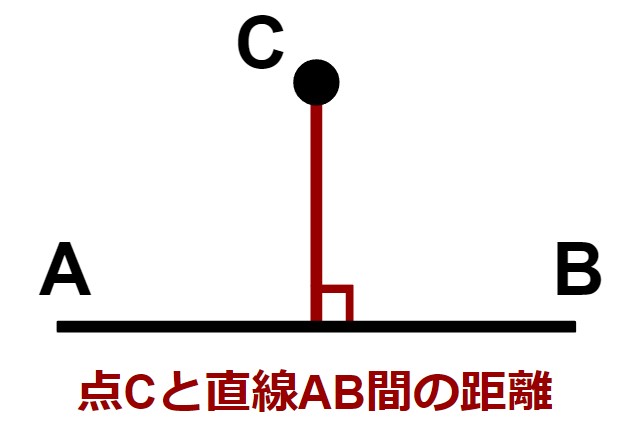
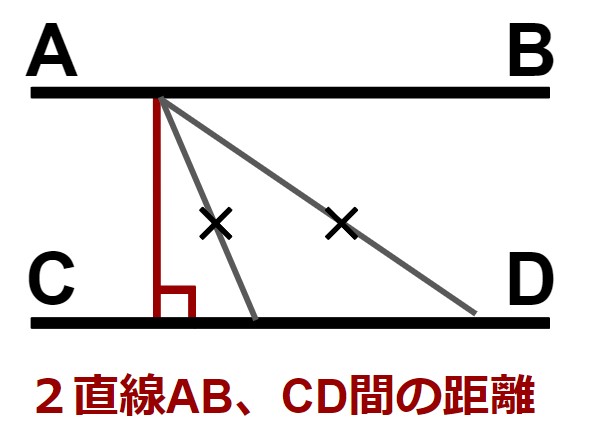
「図形間の距離を求めよ」という問題が出ることがありますが、距離=最短ルートです。
例えば、点と点、点と線、線と線の距離は以下の赤線のようになります。

平行移動
図形や直線を、角度を変えずに移動させることを平行移動と言います。
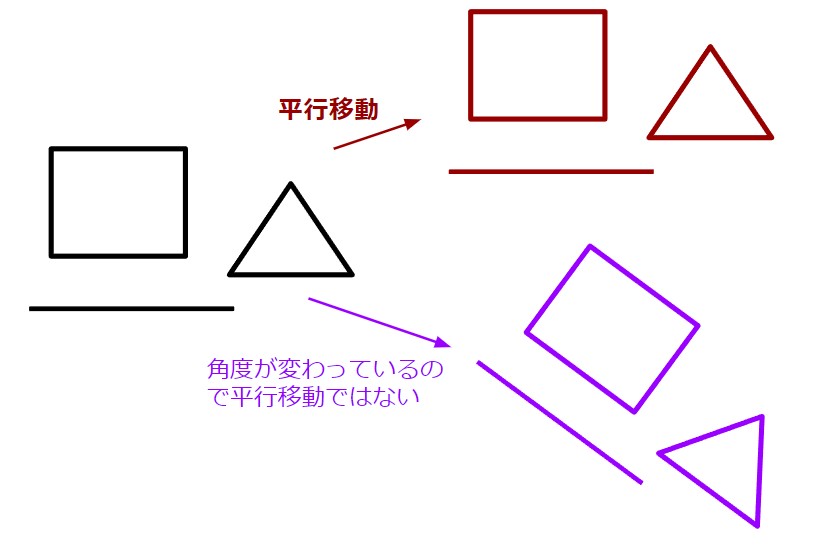
回転移動
図形や直線を、1つの点を中心として回転させて移動させることを回転移動と言います。
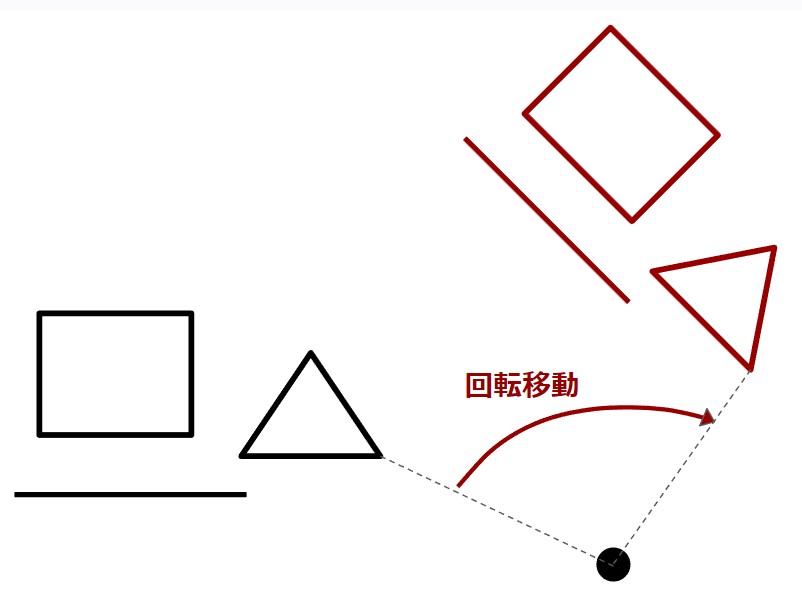
点対称移動
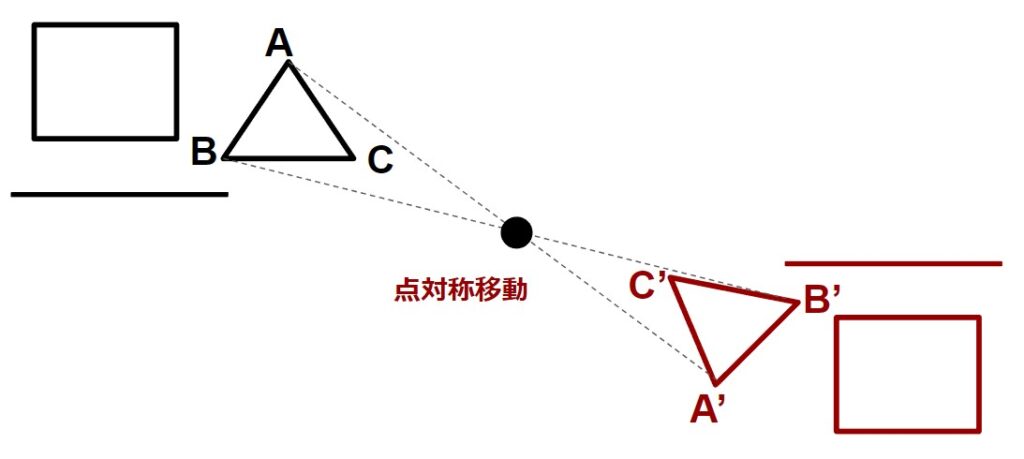
図形を、1つの点に対してちょうど反対側に移動させることを点対称移動と言います。
※実は、点対称移動させた図形は、180°回転移動させた図形と等しくなります。
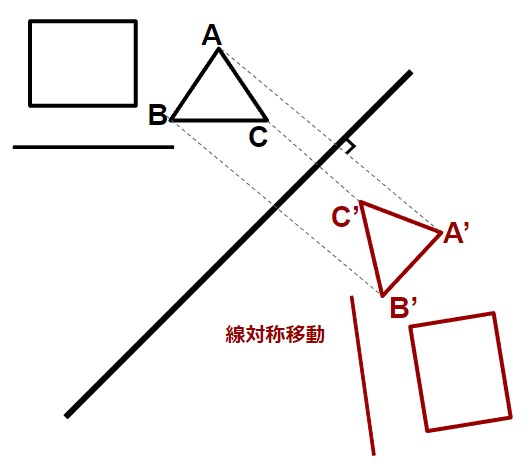
線対称移動
図形を、1つの線に対してちょうど反対側に移動させることを線対称移動と言います。
※鏡に映る像を想像しすればイメージが付きやすいと思います。