多項式の計算(説明ページ)
概要
多項式の計算は、これまで学んできた考え方を応用することで計算することができる。
加法
例えば 2a+b と 3a-2b という2つの多項式を足すことを例にとり、多項式の加法について考えていきましょう。
多項式の加法は、以下の通りカッコ()で多項式を囲んで足すことで計算できます。

次に、(2a+b)+(3a-2b) を計算するためにかっこを外したいのですが、かっこ前が+(正の符号)の場合はかっこをそのまま外すことができます。
※忘れた方は、文字式の計算の準備(説明ページ)で復習しましょう。
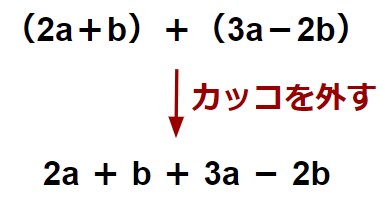
最後に、同類項をまとめ、5a-b となります。

練習問題1
次の2つの多項式を足すために、空欄に入る適切な式を答えなさい。
(1)a+2b, 3a+b
+
=
=
(2)x+y, 2x-y
+
=
=
減法
先ほどと同様、2a+b と 3a-2b という2つの多項式を引くことを例にとり、多項式の減法について考えていきましょう。
多項式の減法は、以下の通りカッコ()で多項式を囲んで引くことで計算できます。

次に、(2a+b)-(3a-2b) を計算するためにかっこを外したいのですが、かっこ前が-(負の符号)の場合はかっこをはずすと、かっこの中の符号が逆になります。
※忘れた方は、文字式の計算の準備(説明ページ)で復習しましょう。
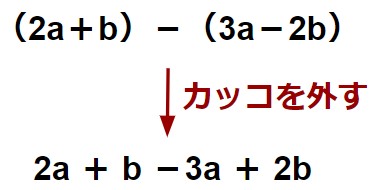
最後に、同類項をまとめ、-a+3b となります。

練習問題2
次の2つの多項式について、左の式から右の式を引くために、空欄に入る適切な式を答えなさい。
(1)a+2b, 3a+b
=-
=
=
(2)x+y, 2x-y
=-
=
=
多項式と数字の乗法
次は、2a+4b と2をかけることを例にとり、多項式と数字の乗法について考えていきましょう。
多項式と数字の乗法は、以下の通り分配法則を用いて計算できます。

この式を計算すると、4a+8b となります。
練習問題3
空欄に入る適切な式を答えなさい。
(1)3(a+2b)
=+
=
(2)5(2a-b)
=+
=
多項式と数字の除法
最後に、2a+4b を2でわることを例にとり、多項式と数字の除法について考えていきましょう。
といっても、除法は逆数をとる事で乗法として考えることができるので、難しい話はありません。

あとは分配法則を用いて計算し、a+2b と計算できます。

練習問題4
空欄に入る適切な式を答えなさい。
(1)(3a+6)÷3
=×
=×+×
=
(2)(3a+6)÷32
=×
=×+×
=