文字式の計算の準備(説明ページ)
概要
- 文字式は項に分解することができる。
- 式を整理したときに、文字の前についている数字を、その文字の係数という。
- 文字式の計算をする際は、分配法則をよく使う。
目次
項と係数
文字式 5a+b-1 という式を記号の手前で分解すると、
5a / +b / -1
と【5a, b, -1】 の3つに分解することができます。(正の符号+は省略可能)
この3つ【5a, b, -1】 のことを、5a+b+1 の項といいます。
各項について、文字の前についている数字を、その文字の係数と言います。
例えば、a の係数は5、bの係数は1です。
※最後の【-1】は文字が入っていないので、係数は存在しません。
項や係数といった用語は重要ですので、必ず覚える用にしましょう。
とりあえずこれだけ覚えて!
- 文字式は項に分解することができる。
- 式を整理したときに、文字の前についている数字を、その文字の係数という。
練習問題1(問題)
a-4b+9 の項を答えなさい。
また、a,bそれぞれの係数を答えなさい。
項:
aの係数:
bの係数:
分配法則
文字式の計算に入っていく前に、文字式の計算をするために必要な数学のルールを勉強していきましょう。
まずは、分配法則です。
分配法則とは、次の式が成り立つという法則です。
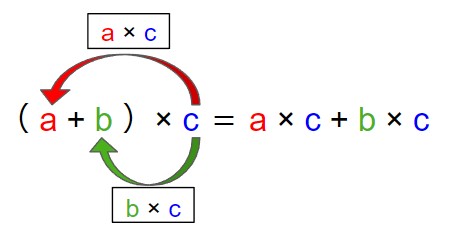
(a+b)× c = a×c + b×c = ac + bc
具体的に数字を代入してみて使い方を確認すると理解しやすいかもしれません。
a=2, b=3, c=4 を代入してみると、分配法則の式は
(a+b)× c
=(2+3)×4
=2×4+3×4
=8+12
=20
となります。
実際に、(2+3)×4=5×4=20であるため、分配法則が成り立つことが確認できました。
とりあえずこれだけ覚えて!
- 分配法則:(a+b)× c = a×c + b×c
それでは、簡単な練習問題を解いてみましょう。
練習問題2(問題)
次の式を、分配法則を用いて計算します。
穴埋めしなさい。
(2+20)×5=×5+×5=+=
普通に (2+20)×5=22×5=・・・と計算していると、暗算では少し難しいですが、分配法則を使うと簡単に計算できましたね。
分配法則を用いることで、このように計算が楽になる場合もあります。さらには、文字式を用いた式変形の際に必ず必要になってくるので、頑張って覚えましょう。
かっこ()の外し方
次はかっこ()の外し方を勉強していきましょう。
文字式では、多くのかっこが登場します。
これから説明するルールを知らないと、間違った答えが出てしまいますので、頑張って覚えましょう。
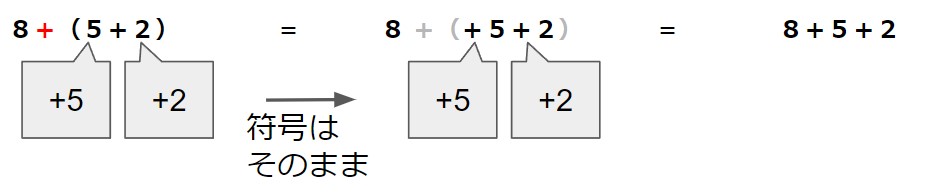
例えば、8+(5+2)という式があったとします。
この計算式の答えは、かっこの中身を先に計算して、8+7=15 となります。
実は、これはかっこを外してしまって、8+5+2を計算しても同じ答えが出ます。
つまり、かっこの前に正の符号(+)がついている場合は、かっこはそのまま外せるのです。
それでは、かっこの前に負の符号(-)がついている場合はどうでしょうか。
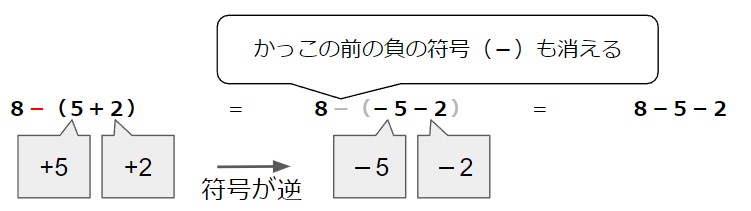
例えば、8-(5+2)という式があったとします。
この計算式の答えは、かっこの中身を先に計算して、8-7=1 となります。
しかし、そのままかっこを外すと 8-5+2=5であり、そのままかっこを外してはいけないことが分かります。
実は、かっこの前に負の符号(-)がついている場合は、かっこを外すときに、かっこの中の符号が逆になるのです。
つまり、8-(5+2)= 8-5-2=1というようにかっこを外します。
とりあえずこれだけ覚えて!
- かっこの前に正の符号(+)がついている場合は、かっこはそのまま外せる。
- かっこの前に負の符号(-)がついている場合は、かっこを外すときにかっこの中の符号が逆になる。
※かっこ()を外すときのルールの理由
基本的に、↑のルールを覚えるだけでかっこ()を外すことができます。
しかし、理由を知りたい人もいると思いますので、簡単に考え方を説明します。
とりあえず今は問題が解ければいい、という方は、練習問題3に進んでください。
結論から説明すると、実は「かっこ()を外す」ことと、「分配法則を使う」ことは同じことをしているのです。
例えば、先ほどの8+(5+2)と 8-(5+2)を例に説明します。
8+(5+2)は、8+(+1)×(5+2)と変形することができます。
つまり、8+(5+2)=8+(+1)×(5+2)=8+(+1)×5+(+1)×2 =8+(+5)+(+2)=8+5+2
であり、分配法則により、かっこの中の数字に(+1)をかけていることが分かります。
(+1)をかけても何も変わらないので、かっこの前に正の符号(+)がついている場合は、かっこはそのまま外せる。ということになります。
同様に 8-(5+2)は、8+(-1)×(5+2)と変形することができます。
つまり、8-(5+2)=8+(-1)×(5+2)=8+(-1)×5+(-1)×2 =8+(-5)+(-2)=8-5-2
であり、分配法則により、かっこの中の数字に(-1)をかけていることが分かります。
(-1)をかけると符号が逆になるので、かっこの前に負の符号(-)がついている場合は、かっこを外すときにかっこの中の符号が逆になる。ということになります。
この考えは応用問題を解くうえで、非常に大切ですので、余裕があれば理解しておきましょう。
それでは、練習問題で練習してみましょう。
練習問題3(問題)
かっこを外して計算しようとしています。
穴埋めしなさい。
(1)3+(3-4)==2
(2)8-(-5-2)==15
練習問題3(解説)
(1)
かっこの前に正の符号(+)がついている場合は、かっこはそのまま外せるので、
3+(3-4)
=3+3-4
=2
答え:2
(2)
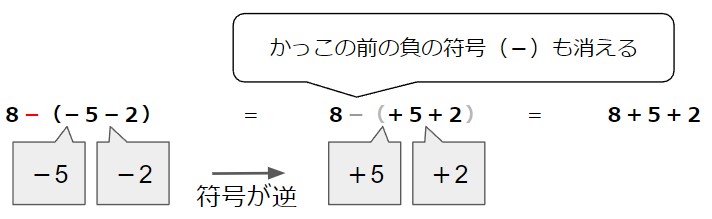
かっこの前に負の符号(-)がついている場合は、かっこを外すときにかっこの中の符号が逆になるので、
8-(-5-2)
=8+5+2
=15
答え:15
練習問題4(問題)
文字式であったとしてもかっこの外し方は同じです。
次の問題を解いてみましょう。
かっこを外して計算しようとしています。
穴埋めしなさい。
(1)a+(2a-4)=
(2)3a-(-2a+2)=
練習問題4(解説)
(1)
かっこの前に正の符号(+)がついている場合は、かっこはそのまま外せるので、
a+(2a-4)
=a+2a-4
答え:a+2a-4
(※この式はもう少し計算し、3a-4と変形することもできます。やり方は次の章で説明します。)
(1)
かっこの前に負の符号(-)がついている場合は、かっこを外すときにかっこの中の符号が逆になるので、
3a-(-2a+2)
=3a+2a-2
答え:3a+2a-2
(※この式はもう少し計算し、5a-2と変形することもできます。やり方は次の章で説明します。)