文字式の計算の準備(基本問題)
※このページは問題ページです。
この範囲の説明は↓で解説していますので、分からなければ先に↓を読んで下さい。
練習問題1
文字式はに分解することができる。
解説
例えば、5a+b-1 という式を記号の手前で分解すると、
5a / +b / -1
と【5a, b, -1】 の3つに分解することができます。(正の符号+は省略可能)
この3つ【5a, b, -1】 のことを、5a+b+1 の項といいます。
練習問題2
各項について、文字の前についている数字を、その文字のという。
解説
例えば、5a+b-1 という式の項は、【5a, b, -1】 の3つです。
各項について、文字の前についている数字を、その文字の係数と言います。
つまり、
・a の係数は5
・bの係数は1
・-1は文字が入っていないので、係数は存在しない
練習問題3
4a-b+10 の項を答えなさい。
また、a,bそれぞれの係数を答えなさい。
項: 4a-b+10 という式を記号の手前で分解すると、 4a / -b / +10 と【4a , -b , +10】 の3つ項に分解することができます。(正の符号+は省略可能) 各項について、文字の前についている数字を、その文字の係数と言います。
aの係数:
bの係数:
解説
つまり、
・a の係数は4
・bの係数は-1
・+10は文字が入っていないので、係数は存在しない
練習問題4
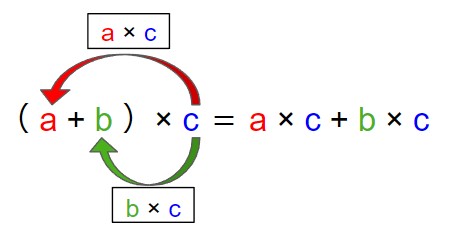
法則とは、次の式が成り立つという法則です。
(a+b)× c = a×c + b×c = ac + bc。
解説
練習問題5
分配法則とは、次の式が成り立つという法則です。
(a+b)× c = += +
練習問題6
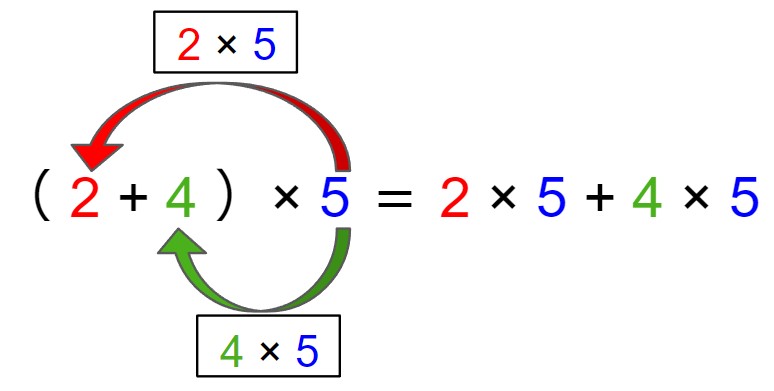
次の式を、分配法則を用いて計算します。
穴埋めしなさい。
(2+4)×5=×5+×5=+=
解説
練習問題7
かっこを外して計算しようとしています。
穴埋めしなさい。
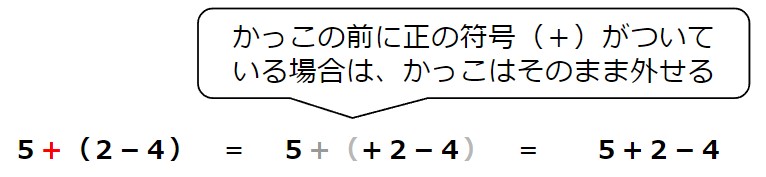
(1)5+(2-4)==
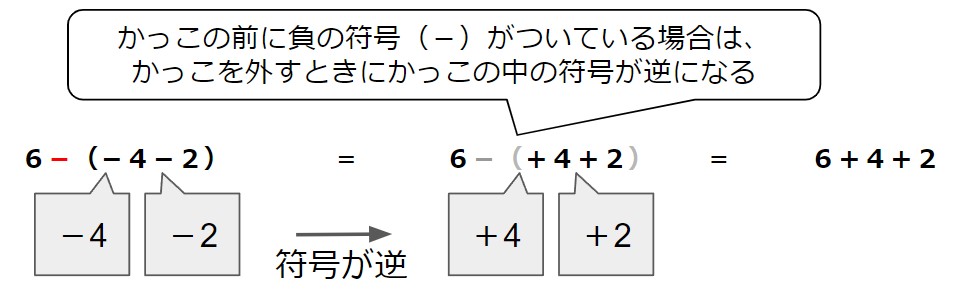
(2)6-(-4-2)==
解説
とりあえずこれだけ覚えて!
- かっこの前に正の符号(+)がついている場合は、かっこはそのまま外せる。
- かっこの前に負の符号(-)がついている場合は、かっこを外すときにかっこの中の符号が逆になる。
問題(1)
問題(2)
練習問題8
かっこを外して計算しようとしています。
穴埋めしなさい。
(1)2a+(3a-5)=
(2)3a-(-a+b)=
解説
問題(1)
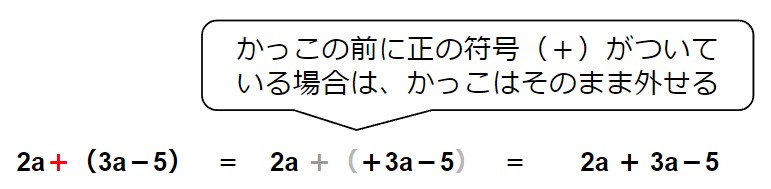
(※この式はもう少し変形し、5a-5と書くこともできます。やり方は次の章で説明します。)
問題(2)
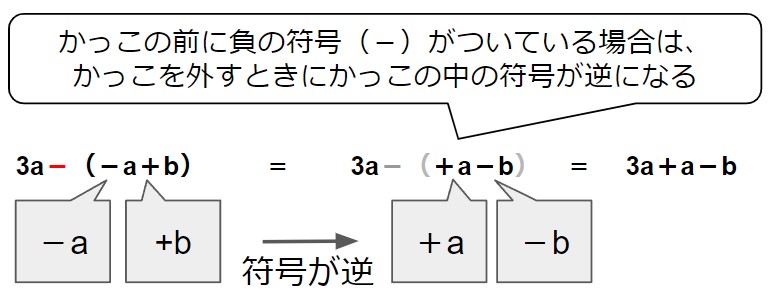
(※この式はもう少し変形し、4a-bと書くこともできます。やり方は次の章で説明します。)