素数(基本問題)
※このページは問題ページです。
この範囲の説明は↓で解説していますので、分からなければ先に↓を読んで下さい。
練習問題1
次の空欄を埋めなさい。
と以外に約数がない自然数を素数という。
なお、1は素数に含め。
練習問題2
次の数が素数かどうかを答えなさい。
(1)4
(2)3
答え:(1)(2)
解説
その数を、その数より小さい数(1以外)で割り切ることができるか、を確認すればよい。
(1)4
4の約数は「1, 2, 4」である。
つまり、4は2で割り切れる。
つまり、4は4より小さい数2で割り切れることが出来るため、素数ではない。
(2)3
3の約数は「1, 3」である。
つまり、3は3と1以外の数字で割り切ることが出来ないため、素数である。
練習問題3
1以上20以下の素数をならべています。
以下の空欄に入る数字を答えなさい
、3、5、、、13、、
練習問題4
自然数を素数の績で表すことを、といいます。
解説
例えば12を素因数分解すると、以下のようになります。
12=2×2×3=22×3(素数である2と3の積として表すことが出来た。)
これが、素因数分解です。
練習問題5
次の数を素因数分解しなさい。
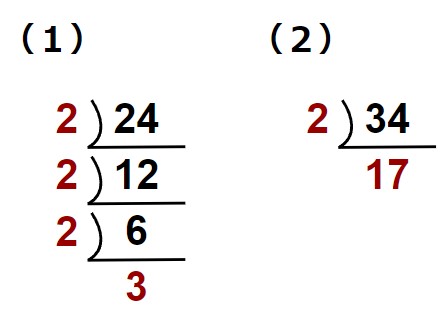
(1)24=×××=×
(2)34=×
解説