比例・反比例(説明ページ)
概要
- 「xを2倍するとyも2倍になる」「xを3倍するとyも3倍になる」、、、といった関係があるとき、「yはxに比例する」と言う。
- 「xを2倍するとyは12倍になる」 「xを3倍するとyは13倍になる」 、、、といった関係があるとき、「yはxに反比例する」と言う。
定数
比例について学ぶ前に、新しい単語を覚えましょう。
決まった値をとる数のことを定数といいます。
関数の説明をしたときに使った以下の例でいうと、変数はx,yで、定数は100です。
- 100円のリンゴの数をx、合計金額をyと置くと、「 y = 100 x 」
つまり、リンゴを買った数と合計金額は変わる(変数)が、リンゴの値段 100円 は変わらない(定数)ということです。
とりあえずこれだけ覚えて!
- 決まった値をとる数のことを定数という。
比例
再び、関数の説明をしたときに使った以下の例を見てみましょう。
100円のリンゴの数をx、合計金額をyと置くと、「 y = 100 x 」と表すことが出来ました。
- xが1の時(リンゴが1個の時)・・・yは100(合計金額が100円)
- xが2の時(リンゴが2個の時)・・・yは200(合計金額が200円)
- xが3の時(リンゴが3個の時)・・・yは300(合計金額が300円)
この時、xとyの変化に注目してみると、「xを2倍するとyも2倍になる」「xを3倍するとyも3倍になる」といった関係があることがわかると思います。
このような関係があるとき、「yはxに比例する」といいます。
つまり、「 y = 100 x 」という関数は、「xを2倍するとyも2倍になる」「xを3倍するとyも3倍になる」といった関係があることを意味し、「yはxに比例する」と言うのです。
より一般化すると、「 y =ax(aは100などの定数)」という関数は、「xを2倍するとyも2倍になる」「xを3倍するとyも3倍になる」といった関係があることを意味し、「yはxに比例する」と言います。
また、y=axの定数aは、特別に比例定数と呼びます。
とりあえずこれだけ覚えて!
- 「xを2倍するとyも2倍になる」「xを3倍するとyも3倍になる」、、、といった関係があるとき、「yはxに比例する」と言う。
- 比例は以下のような関数で表される。
y=ax(aは定数) - aは定数の中でも、特別に比例定数と呼びます。
- 比例は以下のような関数で表される。
練習問題1
yはxに比例し、x=1の時y=3です。
このとき、以下穴埋めしなさい。
(1)x=2の時y=
(2)x=ー3の時y=
(3)関数の形で表すと「y=」と表せる
練習問題1(解説)
(1)(2)
「yはxに比例する」とは、「xを2倍するとyも2倍になる」「xを3倍するとyも3倍になる」といった関係があることを意味します。
つまり、
(1)xを2倍するとyも2倍
(2)xを-3倍するとyも-3倍
になります。
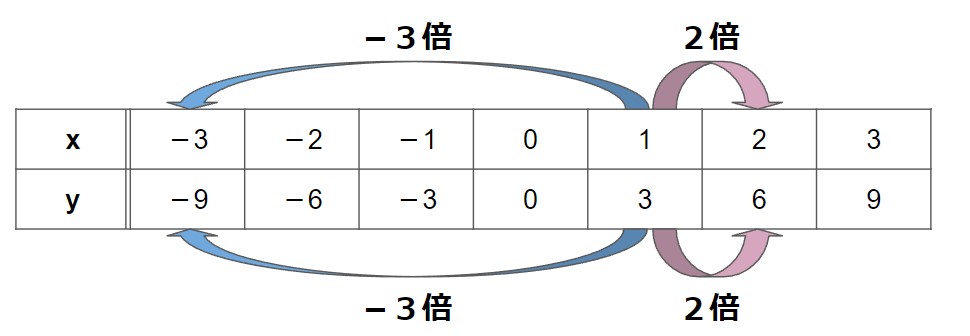
上図の通り、x=1、y=3からスタートして、
(1)xを2倍にして2にすると、yも2倍の6になり、
(2)xを-3倍にして-3にすると、yも-3倍の-9になります。
答え:(1)6(2)-9
(3)
「yはxに比例する」とき「 y =ax(aは100などの定数)」という関数で表すことが出来ます。
問題文から、x=1の時y=3であることがわかるので、 y =ax に代入すると、
y =ax ⇒ 3=a×1=a
となり、aが3であるということが分かります。
つまり、xとyの関係は、 y =3x と表すことが出来ることが分かりました。
答え:3x
反比例
結論から言ってしまうと、比例とは逆で、「xを2倍するとyは12倍になる」「xを3倍するとyは13倍になる」といった関係のことを「yはxに反比例する」と言います。また、反比例は以下のような関数で表されます。
y=ax(aは定数)
この定数aも、比例定数という呼び方をすることがあります。
とりあえずこれだけ覚えて!
-
「xを2倍するとyは12倍になる」
「xを3倍するとyは13倍になる」
、、、といった関係があるとき、「yはxに反比例する」と言う。
-
反比例は以下のような関数で表される。
y=ax(aは定数) - aは定数の中でも、特別に比例定数と呼びます。
-
反比例は以下のような関数で表される。
練習問題2
yはxに反比例し、x=1の時y=3です。
このとき、以下穴埋めしなさい。
(1)x=3の時y=
(2)x=-1の時y=
(3)関数の形で表すと「y=」と表せる
練習問題2(解説)
(1)(2)
つまり、
(1)xを3倍するとyは13倍
(2)xをー1倍するとyはー11倍(つまりー1倍)
になります。
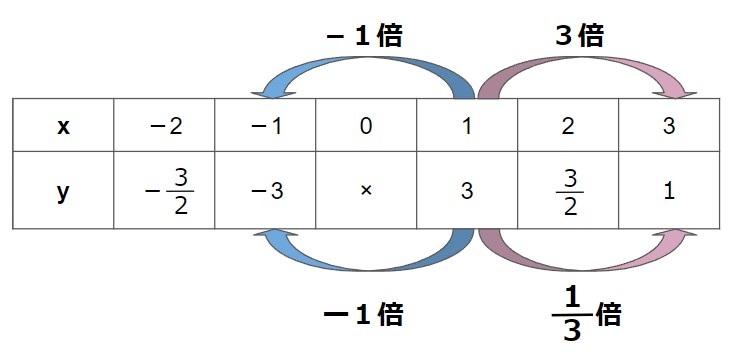
(1)xを3倍にして3にすると、yは13倍の1になり、
(2)xを-1倍にして-1にすると、yは-11倍(つまり-1倍)の-3になります。
答え:(1)1(2)-3
(3)
問題文から、x=1の時y=3であることがわかるので、y=axに代入すると、
y=ax ⇒ 3=a1=a
となり、aが3であるということが分かります。
つまり、xとyの関係は、y=3xと表すことが出来ることが分かりました。
答え:y=3x