比例・反比例のグラフ(説明ページ)
概要
- 2つの数直線を組み合わせた図のことを座標平面と言う。
- 座標平面上で、変数xとyの組み合わせを表したものを座標と言う。
- 関数のxとyの関係を目に見えるように座標平面で表したものをグラフと言う。
- 比例のグラフは以下のような見た目をしている。
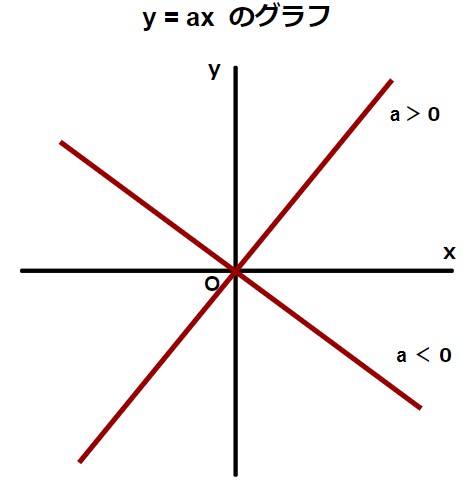
- 反比例のグラフは以下のような見た目をしている。
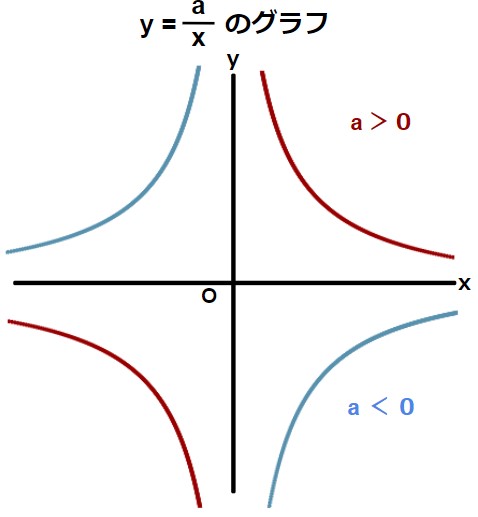
座標
2つの数直線を組み合わせた以下のような図を座標平面と言います。
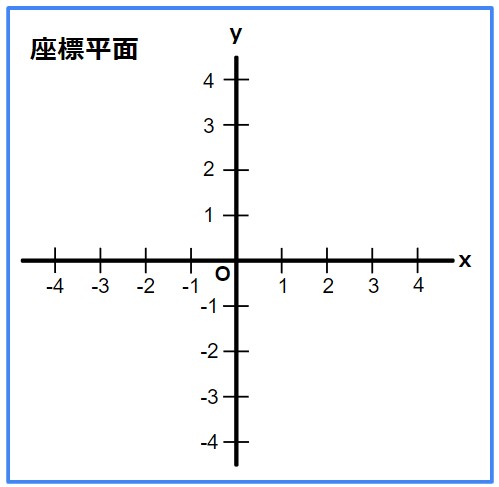
座標の使い方を学ぶ前に、覚えなくてはならない単語がたくさんあるため、まずは以下を覚えてください。
とりあえずこれだけ覚えて!
- 2つの数直線を組み合わせた図のことを座標平面と言う。
- 座標平面上で、変数xとyの組み合わせを表したものを座標と言う。
- 一般的に、xの数直線を横に取りx軸と呼ぶ。また、yの数直線は縦に取りy軸と呼ぶ。
- x軸とy軸の両方を合わせて座標軸と呼ぶ。
- 座標軸が交わる点を原点と言い、アルファベットのOで表す。
- 座標軸に区切られた各エリアのことを、右上から順に、第1象限、第2象限、第3象限、第4象限と呼ぶ。
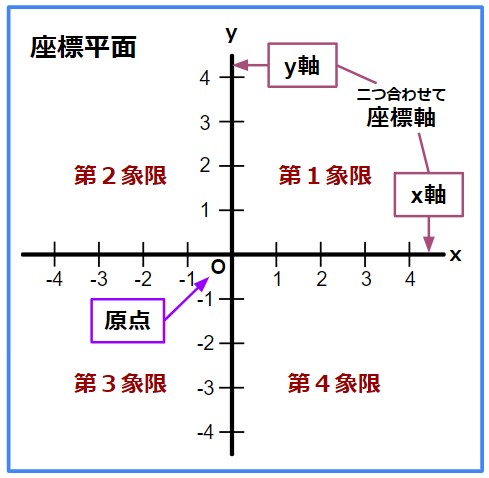
この座標平面を用いることで、変数xとyの組み合わせを表すことが出来るようになります。
例えば、x=3のときy=2という関係を表したければ、以下のように描けます。
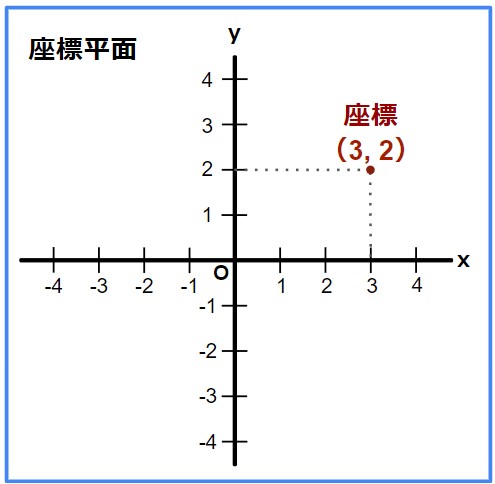
x=3でy=2なので、x軸が3でy軸が2になる点が見つかり、この点のことをx=3,y=2の座標と言います。
また、xの座標のことをx座標、yの座標のことをy座標と言います。(今回はx座標が3、y座標が2)
なお、座標を毎回「x=3,y=2」と書くのは面倒なので、数字の組み合わせで(3, 2)と表します。
とりあえずこれだけ覚えて!
- 座標平面上で、変数xとyの組み合わせを表したものを座標と言う。
- xの座標のことをx座標、yの座標のことをy座標と言う。
- 座標は数字の組み合わせで表すことが出来る。(必ずx座標を左、y座標を右に書く)
比例のグラフ
座標平面を用いると比例の関係を目に見える形で表現することが出来ます。
例えば、y = 2 x という関数では、xとyは比例の関係にあります。
- xが-2の時・・・yは-4
- xが-1の時・・・yは-2
- xが0の時・・・yは0
- xが1の時・・・yは2
- xが2の時・・・yは4
このxとyの組み合わせを座標平面上に座標として表してみると、以下のようになります。
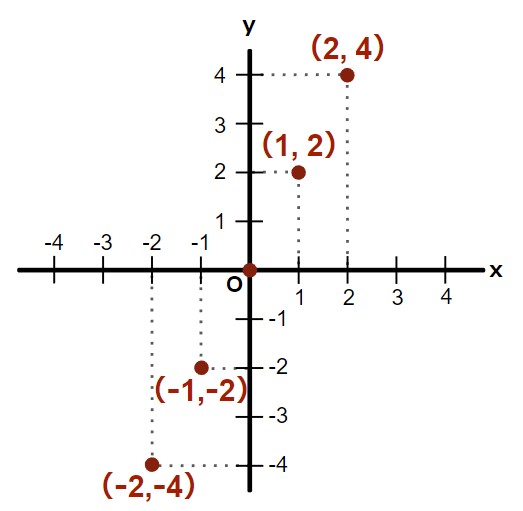
この赤い点を結ぶと、以下のような直線が浮かび上がってきますが、これが y = 2 x のグラフです。
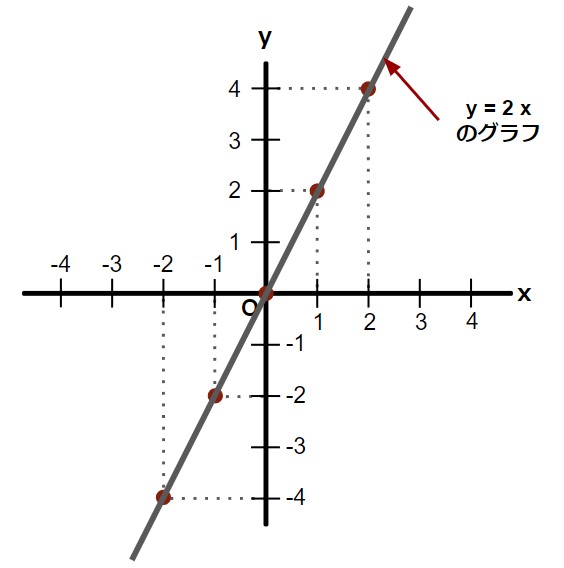
このように、関数 y = ax と表される比例のグラフは、原点を通る直線で表すことが出来ます。
もう一つ例を見てみましょう。
y = ‐x という関数では、xとyは比例の関係にあります。
- xが-2の時・・・yは2
- xが-1の時・・・yは1
- xが0の時・・・yは0
- xが1の時・・・yは1
- xが2の時・・・yは2
このxとyの組み合わせを座標平面上に座標として表して、グラフをかいてみると、以下のようになります。
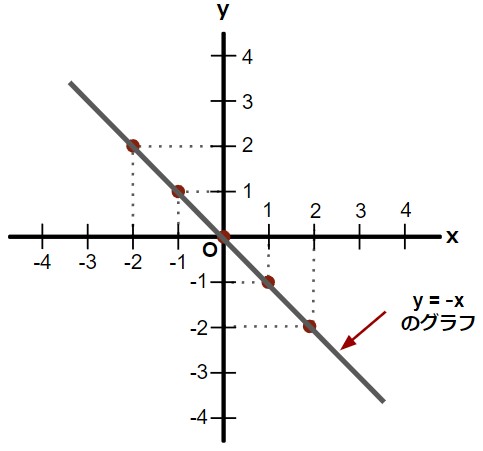
今回も原点を通る直線で表すことが出来ることが確認できましたが、先ほどと直線の向きが違い、右下がりになっていることがわかると思います。
実は、 y = ax のaが0より大きい場合は右上がり、aが0より小さい場合は右下がりの直線になるのです。
とりあえずこれだけ覚えて!
- 比例のグラフは以下のような見た目をしている。

反比例のグラフ
次は、反比例のグラフもかいてみましょう。y=3xという関数では、xとyは反比例の関係にあります。
- xが-3の時・・・yは-33=-1
- xが-2の時・・・yは-32=-1.5
- xが-1の時・・・yは-31=-3
- xが0の時・・・yは30だが、分数の分母は0にならないので、xは0にならない
- xが1の時・・・yは31=3
- xが2の時・・・yは32=1.5
- xが3の時・・・yは33=1
このxとyの組み合わせを座標平面上に座標として表して、グラフをかいてみると、以下のようになります。
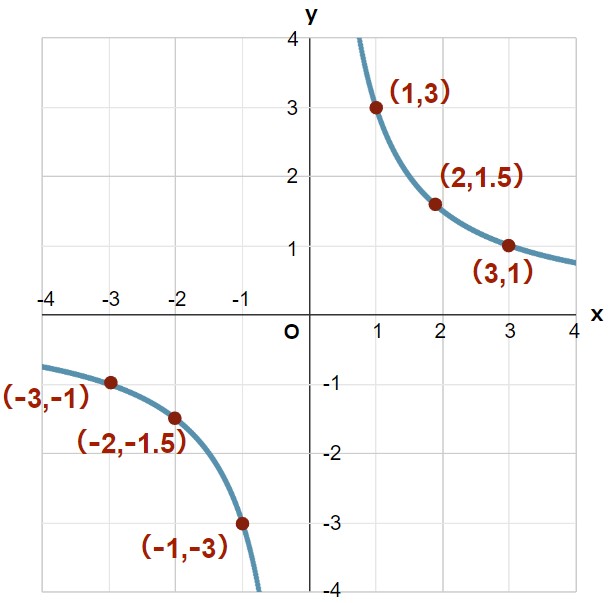
このように、反比例のグラフは曲がった線になります。
また、このような形の曲線のことを数学用語で双曲線と言います。
y=-3xという関数では、xとyは反比例の関係にあります。
- xが-3の時・・・yは33=1
- xが-2の時・・・yは32=1.5
- xが-1の時・・・yは31=3
- xが0の時・・・yは30だが、分数の分母は0にならないので、xは0にならない
- xが1の時・・・yは-31=-3
- xが2の時・・・yは-32=-1.5
- xが3の時・・・yは-33=-1
このxとyの組み合わせを座標平面上に座標として表して、グラフをかいてみると、以下のようば双曲線になります。
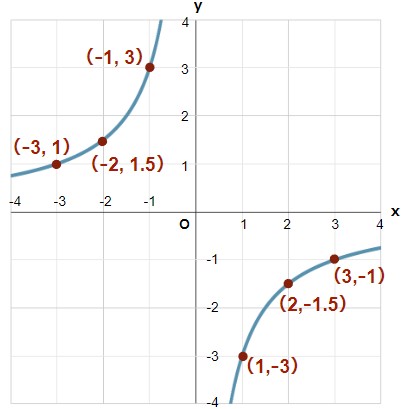
今回も双曲線で表すことが出来ましたが、先ほどと双曲線の位置が異なることがわかると思います。
実は、y=axのaが0より大きいか小さいかにより双曲線の向きが変わるのです。とりあえずこれだけ覚えて!
- 反比例のグラフは以下のような見た目をしている。
