一元一次方程式の解き方(説明ページ)
概要
一元一次方程式を解くには、以下の性質を使って式を変形し、「文字=数字」の形を作り出す必要がある。
① a=b ならば、a+c=b+c
② a=b ならば、a−c=b−c
③ a=b ならば、ac=bc
④ a=b かつ c ≠0ならば a÷c = b÷c
復習
一元一次方程式とはなにか、そして方程式を解くとは何か、をまず知っておく必要があるので、忘れている人のために簡単に復習します。
一元一次方程式
方程式の中でも、1種類の文字しか登場せず、また、累乗(x2やa3)が登場しないもののことを一元一次方程式といいます。
※一元一次方程式の「一元」は「1種類の文字しか登場しない」ということを、「一次」は「3aやx+yなど、累乗(x2や a3)が登場しない」ということを意味します。
例えば、 2a-4=0 は1種類の文字(a)しか登場せず、累乗も登場しないので一元一次方程式です。
方程式を解くとは
方程式が成り立つように、文字に入る値を見つけることを、方程式を解くといいます。
また、方程式を成り立たせる文字の値のことを、方程式の解といいます。
例えば、2a-4=0 という一元一次方程式の文字 a に何を入れたら式が成り立つかを考えると、
a=0を代入:2×0-4=0は成り立たないので×
a=1を代入:2×1-4=0は成り立たないので×
a=2を代入:2×2-4=0は成り立つので〇
ということで、2a-4=0 という一元一次方程式を解くと、解は a=2である、ということになります。
一元一次方程式を解く
それでは、一元一次方程式の解き方を勉強していきましょう。
一元一次方程式を解くには、以下の性質を使って式を変形し、「文字=数字」の形を作り出す必要があります。
① a=b ならば、a+c=b+c
② a=b ならば、a−c=b−c
③ a=b ならば、a×c=b×c
④ a=b かつ c ≠0ならば a÷c = b÷c
式で書いているせいで少し難しく見えるかもしれませんが、簡単に言ってしまうと
「同じ数に、同じ数を足しても・引いても・かけても・わっても、同じ数になる」という性質です。
一つ一つ見ていきましょう。
① a=b ならば、a+c=b+c
「同じ数に、同じ数を足しても、同じ数になる」という性質です。
この性質を使ってどのように一元一次方程式を解くかを、次の方程式を用いて説明します。
x-6=0
考え方
x-6=0 を解く
この式は、x-6は0と等しい、つまり、「x-6と0は同じ数である」という意味である。
そして、x-6と0は同じ数なのであれば、「x-6に6を足した数と0に6を足した数は同じ数である」という性質が成り立つ。
※「同じ数に、同じ数を足しても、同じ数になる」であるため
実際に、「x-6に6を足した数」と「0に6を足した数」を計算してみると
● x-6に6を足した数:x-6+6=x
● 0に6を足した数:0+6=6
つまり、「xと6が同じ数である」という形に変形できるので、x=6が解です。
解:x=6
式をまとめると
x-6=0
x-6+6=0+6
x =6
と変形できることになります。
ここで、最初の式「x-6=0」と最後の式「x=6」を見比べていただきたいのですが、「左辺にあった-6が右辺に移動した」形になっています。
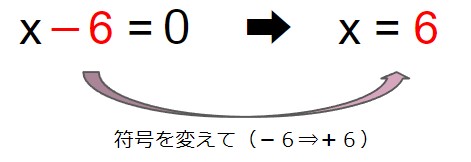
実はこのように、項を反対側に符号を変えて移動させることが出来るのです。
このことを、移項といいます。
とりあえずこれだけ覚えて!
- 項を反対側に符号を変えて移動させることが出来る。このことを移項という。
② a=b ならば、a−c=b−c
「同じ数から、同じ数を引いても、同じ数になる」という性質です。
この性質を使ってどのように一元一次方程式を解くかを、次の方程式を用いて説明します。
x+3=6
考え方
x+3=6 を解く
この式は、x+3は6と等しい、つまり、「x+3と6は同じ数である」という意味である。
そして、x+3と6は同じ数なのであれば、「x+3から3を引いた数と6から3を引いた数は同じ数である」という性質が成り立つ。
※「同じ数から、同じ数を引いても、同じ数になる」であるため
実際に、「x+3から3を引いた数」と「6から3を引いた数」を計算してみると
● x+3から3を引いた数:x+3-3=x
● 6から3を引いた数:6-3=3
つまり、「xと3が同じ数である」という形に変形できるので、x=3が解です。
解:x=3
式をまとめると
x+3=6
x+3-3=6-3
x =3
と変形できることになります。
実は、この式も移項の性質を使って式変形することが出来ます。
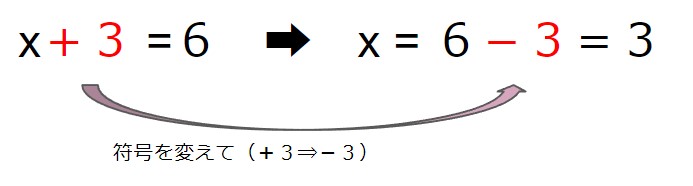
項を反対側に符号を変えて移動させることが出来るという移項するときの性質を確認することが出来ました。
③ a=b ならば、a×c=b×c
「同じ数に、同じ数をかけても、同じ数になる」という性質です。
この性質を使ってどのように一元一次方程式を解くかを、次の方程式を用いて説明します。
考え方はこれまでと同じです。
考え方
そして、 x3 と 2 は同じ数なのであれば、「 x3 に3をかけた数と 2 に3をかけた数は同じ数である」という性質が成り立つ。」
※「同じ数に、同じ数をかけても、同じ数になる」であるため
●x3 に3をかけた数: x3 ×3=x
●2 に3をかけた数は同じ数: 2×3=6
つまり、「xと6が同じ数である」という形に変形できるので、x=6が解です。
解:x=6
式をまとめると
x3 =2x3×3 =2×3
x =6
と変形できることになります。
④ a=b かつ c ≠0ならば a÷c = b÷c
「同じ数を、同じ数でわっても、同じ数になる」という性質です。
なお、 c ≠0ならば という条件が付いているのは、数字を0でわることが出来ないからです。
この性質を使ってどのように一元一次方程式を解くかを、次の方程式を用いて説明します。
考え方はこれまでと同じです。
3x=6
考え方
3x=6 を解く
この式は、3xは6と等しい、つまり、「3xと6は同じ数である」という意味である。
そして、3xと6は同じ数なのであれば、「3xを3でわった数と6を3でわった数は同じ数である」という性質が成り立つ。
※「同じ数を、同じ数でわっても、同じ数になる」であるため
実際に、「3xを3でわった数」と「6を3でわった数」を計算してみると
● 3xを3でわった数:3x ÷3=x
● 6を3でわった数:6÷3=2
つまり、「xと2が同じ数である」という形に変形できるので、x=2が解です。
解:x=2
式をまとめると
3x=6
3x × 13 = 6 × 13x =2
と変形できることになります。
いかがだったでしょうか?
練習してなれるしかないのでとりあえず以下をおぼえて、練習問題で練習していきましょう。
とりあえずこれだけ覚えて!
- 一元一次方程式を解くには、「同じ数に、同じ数を足しても・引いても・かけても・わっても、同じ数になる」という性質を使って式を変形し、「文字=数字」の形を作り出す必要がある。
練習問題1(問題)
次の方程式を解きなさい。
問題A:x-6=3問題B:x+4=5
問題C:x5 =2
問題D:4x=8
練習問題1(解説)
問題A
x-6=3
この式は、x-6は3と等しい、つまり、「x-6と3は同じ数である」という意味である。
そして、x-6と3は同じ数なのであれば、「x-6に6を足した数と3に6を足した数は同じ数である」という性質が成り立つ。
※「同じ数に、同じ数を足しても、同じ数になる」であるため
実際に、「x-6に6を足した数」と「3に6を足した数」を計算してみると
● x-6に6を足した数:x-6+6=x
● 3に6を足した数:3+6=9
つまり、「xと9が同じ数である」という形に変形できるので、x=9が解です。
解:x=9
問題B
x+4=5
この式は、x+4は5と等しい、つまり、「x+4と5は同じ数である」という意味である。
そして、x+4と5は同じ数なのであれば、「x+4から4を引いた数と5から4を引いた数は同じ数である」という性質が成り立つ。
※「同じ数から、同じ数を引いても、同じ数になる」であるため
実際に、「x+4から4を引いた数」と「5から4を引いた数」を計算してみると
● x+4から4を引いた数:x+4-4=x
● 5から4を引いた数:5-4=1
つまり、「xと1が同じ数である」という形に変形できるので、x=1が解です。
解:x=1
問題C
そして、 x5 と 2 は同じ数なのであれば、「 x5 に5をかけた数と 2 に5をかけた数は同じ数である」という性質が成り立つ。」
※「同じ数に、同じ数をかけても、同じ数になる」であるため
●x5 に5をかけた数: x5 ×5=x
●2 に5をかけた数は同じ数: 2×5=10
つまり、「xと10が同じ数である」という形に変形できるので、x=10が解です。
解:x=10
問題D
4x=8 を解く
この式は、4xは8と等しい、つまり、「4xと8は同じ数である」という意味である。
そして、4xと8は同じ数なのであれば、「4xを4でわった数と8を4でわった数は同じ数である」という性質が成り立つ。
※「同じ数を、同じ数でわっても、同じ数になる」であるため
実際に、「4xを4でわった数」と「8を4でわった数」を計算してみると
● 4xを4でわった数:4x ÷4=x
● 8を4でわった数:8÷4=2
つまり、「xと2が同じ数である」という形に変形できるので、x=2が解です。
解:x=2