立体の体積と表面積（説明ページ）

角柱・円柱の体積

角柱・円柱の体積はどちらも
　低面積×高さ
で求められます。
※低面積とは、底面の面積

例えば、以下の角柱の体積は

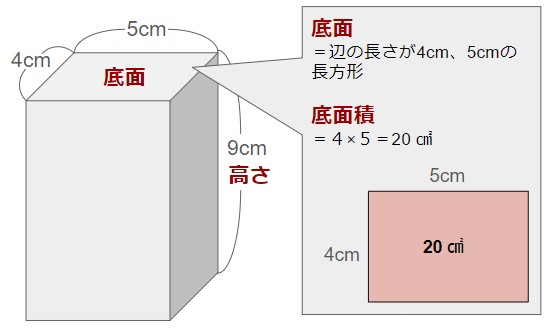
　低面積：４×５＝20 cm²
　高さ：９cm
　⇒ 体積：低面積×高さ＝20×9=180cm³

と求められます。

円柱の場合も同様で、例えば、以下の円柱の体積は

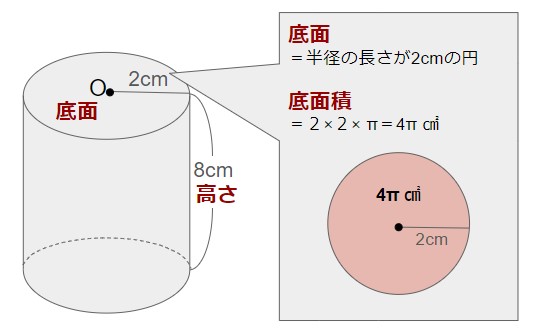
　低面積：２×２× π＝4π cm²
　高さ：８cm
　⇒ 体積：低面積×高さ＝4π×８=32cm³

と求められます。

角錐・円錐の体積

角錐・円錐の体積はどちらも
　低面積×高さ×13
で求められます。

例えば、以下の角錐の体積は

　低面積：４×５＝20 cm²
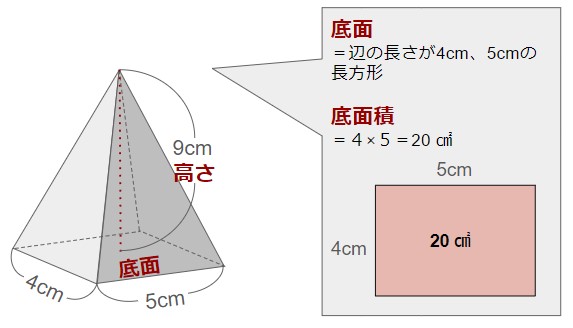
　高さ：９cm
　⇒体積：低面積×高さ×13＝20×9×13=60cm³

と求められます。

円錐の場合も同様で、以下の円錐の体積は

　低面積：２×２× π＝4π cm²
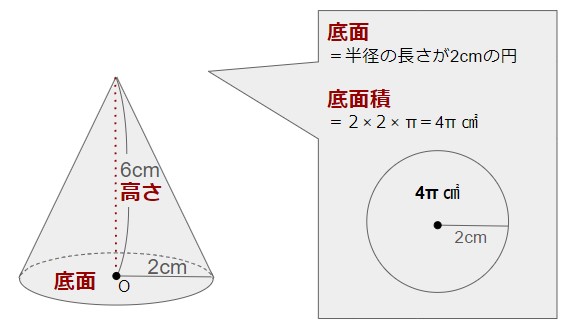
　高さ：６cm
　体積：低面積×高さ×13＝4π×6×13=8πcm³

と求められます。

角柱・角錐の表面積

角柱の表面積は、展開図を使って求められます。

例えば、以下の角柱の表面積は

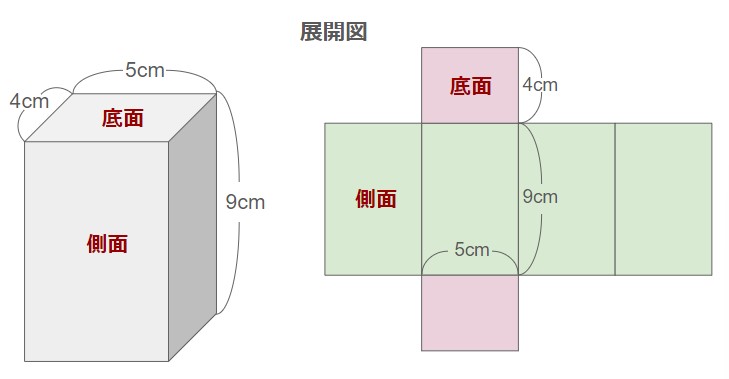
　低面積：４×５＝20 cm²　（２つ）
　側面積：５×９＝45 cm²　（４つ）
　⇒ 表面積：20×2＋45×４=220 cm²

と求められます。

角錐の表面積も同様に、展開図を使って求めることができます。
例えば以下の角錐は

　低面積：４×４＝16 cm²　（１つ）
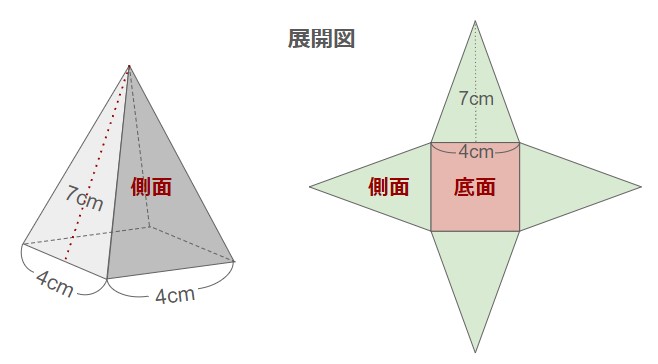
　側面積：4×7×12＝14 cm²　（４つ）
　⇒表面積：16×１＋14×４=72 cm²

と求められます。

円柱の表面積

円柱の表面積も、角柱の表面積と同様に、展開図を使って求めることができます。
例えば以下の円柱は

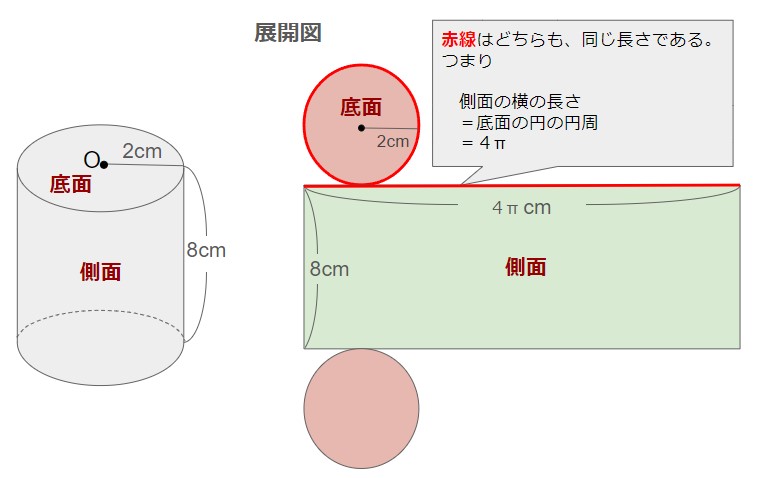
　低面積：２×２×π＝4π cm²　（２つ）
　側面積：4π×8＝32π cm²　（１つ）
　⇒ 表面積：4π×2＋32π=40π cm²

と求められます。
しかし、このように、円柱の表面積を求めるステップは少し複雑です。
そこで、以下の公式を覚えるといいでしょう。

例えば、先ほどの円柱（底面の半径2、高さ8）の場合、公式を使うと
　表面積＝2πr(h+r)＝2×π×2×(8+2)＝40π cm²
と求めることが出来ます。

円錐の表面積

円錐の表面積も、角柱の表面積と同様に、展開図を使って求めることができます。
例えば以下の円錐は

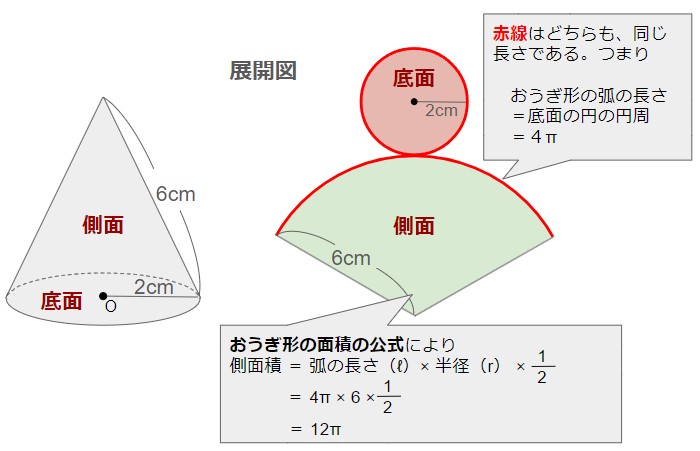
　低面積：２×２×π＝4π cm²　（１つ）
　側面積：12π cm²　（１つ）
　⇒ 表面積：4π＋12π=16π cm²

と求められます。
しかし、このように、円錐の表面積を求めるステップは少し複雑です。
そこで、以下の公式を覚えるといいでしょう。

例えば、先ほどの円錐（底面の半径2、母線6）の場合、公式を使うと
　表面積＝πr(L+r)＝π×2×(6+2)＝16π cm²
と求めることが出来ます。

球の体積・表面積

※高校数学を使えば証明できますが、今は以下の公式を丸暗記してください。

例えば、以下の球の体積・表面積は

　体積：43π×3×3×3＝36π cm³

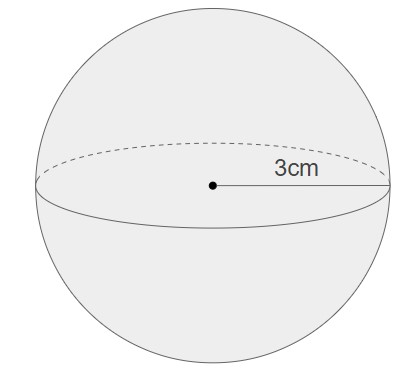
　表面積：４π×3×3 = 36π cm²

と求められます。