立体の体積と表面積(基本問題)
※このページは問題ページです。
この範囲の説明は↓で解説していますので、分からなければ先に↓を読んで下さい。
練習問題1
-
角柱の体積
× -
角錐・円錐の体積
×× -
角柱・角錐の表面積
を用いて求める -
円柱の表面積
底面の半径 r 、高さ h の円柱の表面積
-
円錐の表面積
底面の半径 r 、母線 L の円錐の表面積
-
球の体積
半径 r の球の体積
-
球の表面積
半径 r の球の表面積
練習問題2
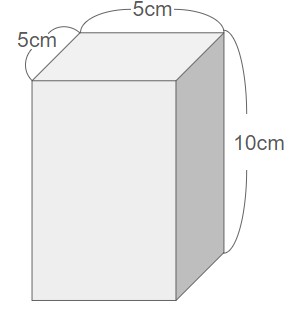
上記の角柱の体積を求めよ。
底面積:×=cm2
高さ:cm
⇒体積:×=×=cm3
練習問題3
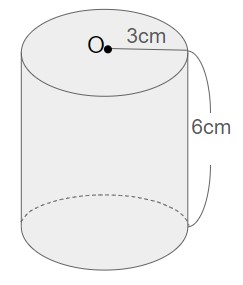
上記の円柱の体積を求めよ。
底面積:××=cm2
高さ:cm
⇒体積:×=×=cm3
練習問題4
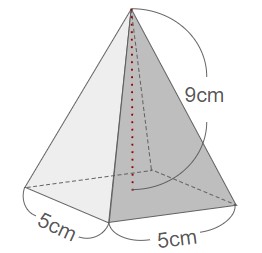
上記の角錐の体積を求めよ。
底面積:×=cm2
高さ:cm
⇒体積:××
=××
=cm3
練習問題5
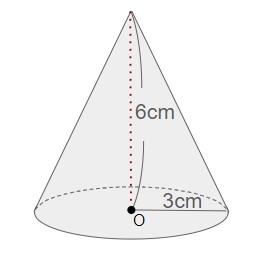
上記の円錐の体積を求めよ。
底面積:××=cm2
高さ:cm
⇒体積:××
=××
=cm3
練習問題6

上記の角柱の表面積を求めよ。
底面積:×=cm2
側面積:×=cm2
⇒底面が面、側面が面あるので、表面積は
(×)+(×)
=+
=cm2
練習問題7
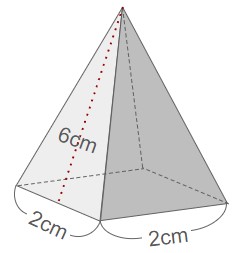
上記の角錐の表面積を求めよ。
低面積:×=cm2
側面積:××
=cm2
⇒底面が面、側面が面あるので、表面積は
(×)+(×)
=+
=cm2
練習問題8

上記の円柱の表面積を求めよ。
低面積:××=cm2
側面を広げた時の横の長さ==××=
側面積:×=
⇒底面が面、側面が面あるので、表面積は
(×)+(×)
=+
=cm2
+α
底面の半径 r 、高さ h の円柱の表面積が
2πr(h+r)
で表されるという公式を知っていると
表面積=2πr(h+r)=2×π×3×(6+3)=54 π cm2
とかんたんに求めることが出来る。
練習問題9
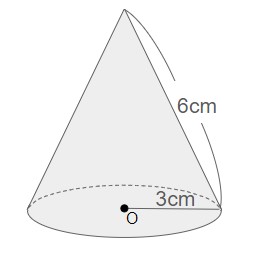
上記の円錐の表面積を求めよ。
低面積:××=cm2
側面積:××=
⇒底面も側面も面だけなので、表面積は
=+
=cm2
解説、+α
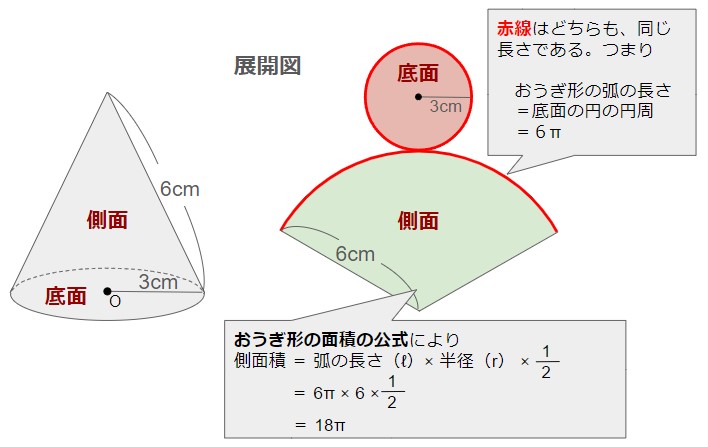
なお、底面の半径 r 、母線 L の円錐の表面積が
πr(L+r)
で表されるという公式を知っていると
表面積=πr(L+r)=π×3×(6+3)=27 π cm2
とかんたんに求めることが出来る。
練習問題10
半径 r の球の体積:
半径 r の球の表面積:
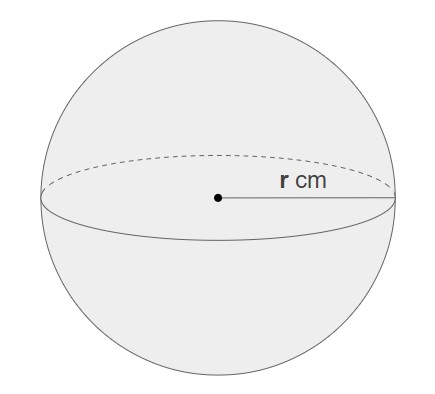
練習問題11
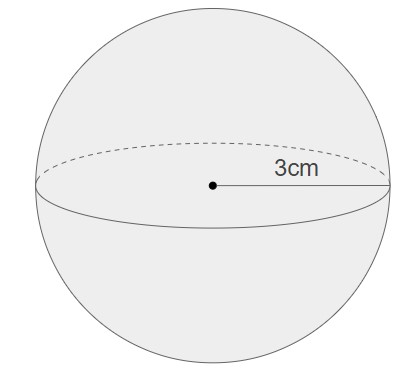
上記の球の体積と表面積を求めよ。
公式に当てはめると、
体積
××3
=cm3
表面積
×2
= cm2