比例式の解き方(説明ページ)
概要
比例式(a:b=c:d)は以下のように変形することが出来る。
① ab = cd② ba = dc
③ a×d=b×c
(復習)比とは
比と、「大きさの割合」つまり、2つ以上のものの大きさを比べるために使用します。
例えば、塩を小さじ3杯、砂糖を小さじ1杯入れる料理があったとします。
この時、砂糖と塩の量を日本語で表すと
「塩を砂糖の3倍入れる必要がある」
となります。
これを数学の比で表すと
「塩:砂糖=3:1」
となります。
比例式とは
結論から言うと、比例式は、比を等号(=)で結んだ式のことです。
例えば「3:1=6:2」のような式です。
とりあえずこれだけ覚えて!
- 比例式は、比を等号(=)で結んだ式のこと。
比例式の意味
この比例式は何を表すための式なのかを説明していきます。
1人前で「塩を小さじ3杯、砂糖を小さじ1杯」とメニューに書いてあったとします。
この料理を3人前作ろうとした場合、「塩は3×3=9杯」「砂糖は1×3=3杯」必要になります。
これを表した式が比例式であり、以下のように表せます。
「塩:砂糖=3:1=9:3」
比例式の解き方
比例式の問題では、比例式の一部が不明なので求めてください、という問題が多いです。
例えば、先ほどの料理の例の場合、以下のような問題として出題されることになります。
式だけの問題
xの値を求めなさい。
- 3:1=9:x
答え:3
文章問題
塩と砂糖を3:1の割合で入れる料理があります。
塩を小さじ9杯入れるとき、砂糖は小さじ何杯入れる必要があるでしょうか。
答え:3杯
さて、実際に試験でこの問題が出題されたときはどのように解くべきでしょうか?
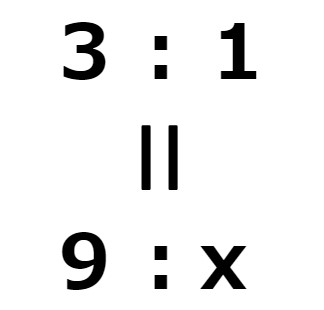
3:1ということは、左側が右側の3倍、、、つまりxを3倍したら9になるから、、、3倍して9になる数は、、、9÷3=3
と考えて解くことももちろんできますが、数が大きくなったり、式が複雑になるとミスも増えてくると思います。
そこで、以下のルールを用いて式を変形し、解くのが一般的です。
とりあえずこれだけ覚えて!
比例式(a:b=c:d)は以下のように変形することが出来る。
① ab = cd② ba = dc
③ a×d=b×c
つまり、3:1=9:xという比例式は
① 31 = 9x② 13 = x9
③ 3×=9
と変形できます。
+α
なぜこのように変形できるかは詳しく説明しませんが、ざっくり以下のように考えると導けます。
- ①は比を分数に直しただけ
- ②は①を逆数にしただけ
- ①②の両辺に分母の数をかけたものが③
詳しく知りたい方は、教科書を読んでください。
それでは、練習問題で比例式の解き方を練習しましょう。
練習問題1(問題)
xの値を求めなさい。
4:5=12:x
練習問題1(解説)
考え方
4:5=12:x
比例式(a:b=c:d)は a×d=b×c と変形できるため、「4:5=12:x」は「4x=5×12」と変形できます。
4x=5×12 を解くと、
- 4x=60
- x=15(解き方を忘れた人は【一元一次方程式の解き方】を確認)
となり、答えはx=15となります。
答え:15